
| A. | $a=\sqrt{3}$,b=1 | |
| B. | 函数f(x)在区间$[{\frac{π}{6},π}]$上单调递增 | |
| C. | 函数f(x)的图象的一个对称中心为$({\frac{2}{3}π,0})$ | |
| D. | 不等式f(x1)f(x2)≤4取到等号时|x2-x1|的最小值为2π |
分析 将函数f(x)化简,f(x1)f(x2)≤4恒成立,f(x)的最大值为2,即a2+b2=4.由于f(x)图象的对称轴为直线$x=-\frac{π}{6}$,可得$f({-\frac{π}{6}})=-\frac{1}{2}a-\frac{{\sqrt{3}}}{2}b$,求解a,b的值.可得解析式.从而根据正弦函数的图象及性质可得答案.
解答 解:函数f(x)=asinx-bcosx
化简可得$f(x)=asinx-bcosx=\sqrt{{a^2}+{b^2}}sin({x-φ})$(其中$tanφ=\frac{b}{a}$),
∵f(x1)f(x2)≤4,∴f(x)的最大值为2,∴a2+b2=4①
由于f(x)图象的对称轴为直线$x=-\frac{π}{6}$,
∴$f({-\frac{π}{6}})=-\frac{1}{2}a-\frac{{\sqrt{3}}}{2}b$,
∴$|{-\frac{1}{2}a-\frac{{\sqrt{3}}}{2}b}|=\sqrt{{a^2}+{b^2}}$②,
由①②解得a=1,$b=\sqrt{3}$.∴$f(x)=2sin({x-\frac{π}{3}})$,
故A错误.
由正弦函数的图象及性质可得:在区间$[{\frac{π}{6},\frac{5π}{6}}]$单调递增,在区间$({\frac{5}{6}π,π}]$上单调递减,故B错误.
将对称中心为$({\frac{2}{3}π,0})$,解析式不成立,故C错误.
当f(x1)f(x2)≤4取到等号时,f(x)能取到两个最大值2,最小间隔为一个周期2π,故选D.
故选D
点评 本题主要考查对三角函数的化简能力和三角函数的图象和性质的运用,利用三角函数的性质求解出符合题意的解析式是解决本题的关键.属于中档题.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({-∞,-\frac{1}{4}}]$ | B. | $[{-\frac{1}{4},+∞})$ | C. | $({-∞,-\frac{3}{4}}]$ | D. | $[{-\frac{3}{4},+∞})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
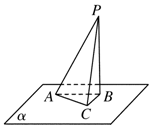 如图所示,三棱锥P-ABC的底面在平面α内,且AC⊥PC,平面PAC⊥平面PBC,点P,A,B是定点,则动点C的轨迹是( )
如图所示,三棱锥P-ABC的底面在平面α内,且AC⊥PC,平面PAC⊥平面PBC,点P,A,B是定点,则动点C的轨迹是( )| A. | 一条线段 | B. | 一条直线 | ||
| C. | 一个圆 | D. | 一个圆,但要去掉两个点 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$ | B. | -2 | C. | $\frac{1}{2}$ | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com