
分析 (1)利用已知取n=1,n=2列出方程,解出即可得出.
(2)利用递推关系与“累乘求积”即可证明.
(3)由an=n,可得${b_n}={2^{a_n}}={2^n}$,当${a_i}+{b_j}={2^n}$时,${b_j}={2^j}$为偶数,可得${a_i}={2^n}-{2^j},1≤j≤n-1$,
因此使得${a_i}+{b_j}={2^n}$成立的所有ai,bj之和S(2n)=(n-1)•2n,令T=S(22)+S(23)+S(24)+…+S(2n),利用“错位相减法”与求和公式即可得出.
解答 (1)解:∵$n=1,{a_1}{a_2}=2=\frac{A+B+2}{3},n=2,{a_1}{a_2}+{a_2}{a_3}=8=\frac{8A+4B+2}{3}$,
∴A=1,B=3.
(2)证明:∵${a_1}{a_2}+{a_2}{a_3}+…+{a_n}{a_{n+1}}=\frac{{{n^3}+3{n^2}+2n}}{3}$,
∴${a_1}{a_2}+{a_2}{a_3}+…+{a_{n-1}}{a_n}=\frac{{{{({n-1})}^3}+3{{({n-1})}^2}+2({n-1})}}{3}({n≥2})$,
两式相减得anan+1=n(n+1)(n≥2),则an+1an+2=(n+1)(n+2),
两式相除得$\frac{{{a_{n+2}}}}{a_n}=\frac{n+2}{n}({n≥2})$,
∴n为偶数时,${a_n}=\frac{a_n}{{{a_{n-2}}}}•\frac{{{a_{n-2}}}}{{{a_{n-4}}}}•…•\frac{a_4}{a_2}•{a_2}=\frac{n}{n-2}•\frac{n-2}{n-4}•…•\frac{4}{2}•2=n$,
n为奇数时,${a_n}=\frac{a_n}{{{a_{n-2}}}}•\frac{{{a_{n-2}}}}{{{a_{n-4}}}}•…•\frac{a_3}{a_1}•{a_1}=\frac{n}{n-2}•\frac{n-2}{n-4}•…•\frac{3}{1}•1=n$,
∴an=n(n≥4),又a1=1,a2=2,a3=3,
∴an=n,
∴数列{an}成等差数列.
(3)解:∵an=n,∴${b_n}={2^{a_n}}={2^n}$,
当${a_i}+{b_j}={2^n}$时,∵${b_j}={2^j}$为偶数,则${a_i}={2^n}-{2^j},1≤j≤n-1$,
∴使得${a_i}+{b_j}={2^n}$成立的所有ai,bj之和S(2n)=(n-1)•2n,
令T=S(22)+S(23)+S(24)+…+S(2n),
则T=22+2×23+3×24+4×25+…+(n-1)×2n,(1)
2T=23+2×24+3×25+…+(n-2)×2n+(n-1)×2n+1,(2)
(1)-(2):-T=22+23+24+…+2n-(n-1)×2n+1=$\frac{{4(1-{2^{n-1}})}}{1-2}-(n-1)×{2^{n+1}}$=-4-(n-2)•2n+1,
∴T=S(22)+S(23)+S(24)+…+S(2n)=(n-2)•2n+1+4.
点评 本题考查了等差数列的通项公式及其求和公式、“错位相减法”、递推关系,考查了分类讨论方法、推理能力与计算能力,属于难题.


 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,2) | B. | (-2,-1) | C. | ($\frac{1}{2}$,1) | D. | (-∞,1)∪(2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
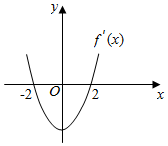
| A. | 0 | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 2 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | |$\overrightarrow{a}$|>|$\overrightarrow{b}$| | B. | |$\overrightarrow{a}$|<|$\overrightarrow{b}$| | C. | |$\overrightarrow{a}$|=|$\overrightarrow{b}$| | D. | $\overrightarrow{a}$=$\overrightarrow{b}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,底面ABCD是等腰梯形,AB∥DC,∠ADC=$\frac{π}{3}$,
如图,在四棱锥P-ABCD中,底面ABCD是等腰梯形,AB∥DC,∠ADC=$\frac{π}{3}$,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com