
| A�� | 0 | B�� | 1 | C�� | 2 | D�� | 3 |
���� �����D����Ϊ$\sqrt{3}$�ĵ�P�γ���D1ΪԲ�ģ��뾶Ϊ$\sqrt{2}$��$\frac{1}{4}$Բ��MN�����û�����ʽ���ɵý��ۣ�
�ڵ�P��A1����C1��ʱ��DP����ACC1A1���ɽǡ�DA1O�����DC1O��������ֵΪ$\frac{{\sqrt{6}}}{3}$��С����P��O1ʱ��DP����ACC1A1���ɽǡ�DO1O������ֵΪ$\sqrt{2}$��ɵ�����ֵȡֵ��Χ��$[{\frac{{\sqrt{6}}}{3}��\sqrt{2}}]$��
����P��x��y��1������x2+y2+1=3����x2+y2=2���ɵ�DP��ǰ�����ҡ��������ϵ���ͶӰ������������������ϵ���ͶӰ����֮�ͣ�
��� 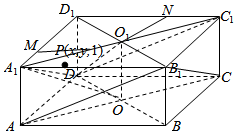 �⣺��ͼ���ٴ������D����Ϊ$\sqrt{3}$�ĵ�P�γ���D1ΪԲ�ģ��뾶Ϊ$\sqrt{2}$��$\frac{1}{4}$Բ��MN������Ϊ$\frac{1}{4}•2��•\sqrt{2}$=$\frac{\sqrt{2}}{2}��$��
�⣺��ͼ���ٴ������D����Ϊ$\sqrt{3}$�ĵ�P�γ���D1ΪԲ�ģ��뾶Ϊ$\sqrt{2}$��$\frac{1}{4}$Բ��MN������Ϊ$\frac{1}{4}•2��•\sqrt{2}$=$\frac{\sqrt{2}}{2}��$��
�ڴ�����Ϊ��A1DC1����ACB1�����Ե�P��������Խ���A1C1���˶�����P��A1����C1��ʱ��DP����ACC1A1���ɽǡ�DA1O�����DC1O��������ֵΪ$\frac{{\sqrt{6}}}{3}$��С����P��O1ʱ��DP����ACC1A1���ɽǡ�DO1O������ֵΪ$\sqrt{2}$�����������ֵȡֵ��Χ��$[{\frac{{\sqrt{6}}}{3}��\sqrt{2}}]$��
����ȷ����P��x��y��1������x2+y2+1=3����x2+y2=2��DP��ǰ�����ҡ��������ϵ���ͶӰ���ֱ�Ϊ$\sqrt{{y^2}+1}��\sqrt{{x^2}+1}��\sqrt{{x^2}+{y^2}}$�������������ϵ���ͶӰ����֮��Ϊ$2��\sqrt{{y^2}+1}+\sqrt{{x^2}+1}+\sqrt{2}����2��2\sqrt{\frac{{{y^2}+1+{x^2}+1}}{2}}+\sqrt{2}��=6\sqrt{2}$�����ҽ���P��O1ʱȡ�Ⱥţ�
��ѡB��
���� ���������������ж�Ϊ���壬�����˹켣���⡢����ǡ���ͶӰ��֪ʶ�㣬�ۺ���ǿ���ѶȽϴ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
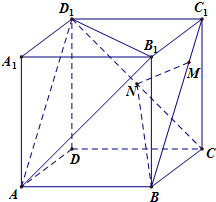 ��ͼ��������ABCD-A1B1C1D1���ⳤΪ1��NΪCD1�е㣬MΪ�߶�BC1�ϵĶ��㣬��M����B��C1�غϣ����ĸ����⣺
��ͼ��������ABCD-A1B1C1D1���ⳤΪ1��NΪCD1�е㣬MΪ�߶�BC1�ϵĶ��㣬��M����B��C1�غϣ����ĸ����⣺�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | $\sqrt{3}$ | C�� | 1 | D�� | $\frac{\sqrt{3}}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
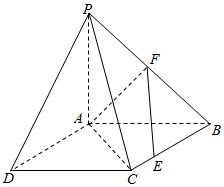 �ı���ABCD�������Σ���PAB���PAD������AΪֱ�Ƕ���ĵ���ֱ�������Σ���F��PB���е㣬��E�DZ�BC�ϵ�����һ�㣮
�ı���ABCD�������Σ���PAB���PAD������AΪֱ�Ƕ���ĵ���ֱ�������Σ���F��PB���е㣬��E�DZ�BC�ϵ�����һ�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
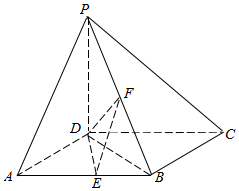 ��ͼ��������P-ABCD�У�PD�͵���ABCD������ABCDΪ�����Σ�PD=DC��E��F�ֱ���AB��PB�ϣ���BE��AE=1��2��PF��BF=2��1��
��ͼ��������P-ABCD�У�PD�͵���ABCD������ABCDΪ�����Σ�PD=DC��E��F�ֱ���AB��PB�ϣ���BE��AE=1��2��PF��BF=2��1���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 2015��7��9��21ʱ15�֣�̨�硰���������ҹ��㶫ʡ½���м����غ���½�����165.17�������֣�5.6���˽���ת�ư��ã�288�䷿�ݵ�����46.5ǧ����ũ�����֣�ֱ�Ӿ�����ʧ12.99��Ԫ������½����222ǧ��÷��Ҳ�ܵ���̨���Ӱ�죬�ʷ���٣�С��������÷��ijС����50����������̨����ɵľ�����ʧ�����ռ������ݷֳ�[0��2000]����2000��4000]����4000��6000]����6000��8000]����8000��10000]���飬��������ͼƵ�ʷֲ�ֱ��ͼ��
2015��7��9��21ʱ15�֣�̨�硰���������ҹ��㶫ʡ½���м����غ���½�����165.17�������֣�5.6���˽���ת�ư��ã�288�䷿�ݵ�����46.5ǧ����ũ�����֣�ֱ�Ӿ�����ʧ12.99��Ԫ������½����222ǧ��÷��Ҳ�ܵ���̨���Ӱ�죬�ʷ���٣�С��������÷��ijС����50����������̨����ɵľ�����ʧ�����ռ������ݷֳ�[0��2000]����2000��4000]����4000��6000]����6000��8000]����8000��10000]���飬��������ͼƵ�ʷֲ�ֱ��ͼ��| ������ʧ������4000Ԫ | ������ʧ����4000Ԫ | �ϼ� | |
| ����500Ԫ | 30 | ||
| ������500Ԫ | 6 | ||
| �ϼ� |
| P��K2��k�� | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com