
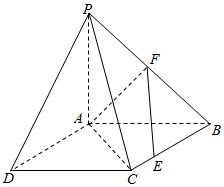
 四边形ABCD是正方形,△PAB与△PAD均是以A为直角顶点的等腰直角三角形,点F是PB的中点,点E是边BC上的任意一点.
四边形ABCD是正方形,△PAB与△PAD均是以A为直角顶点的等腰直角三角形,点F是PB的中点,点E是边BC上的任意一点.分析 (1)由已知得PA⊥AD,PA⊥AB,AB⊥BC,从而PA⊥BC,进而BC⊥面PAB,又AF⊥PB,由此能证明AF⊥EF.
(2)以A为原点,AD为x轴,AB为y轴,P为z轴,建立空间直角坐标系,利用向量法能求出二面角A-PC-B的平面角.
解答 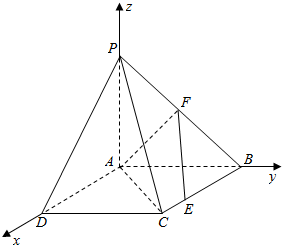 (1)证明:∵四边形ABCD是正方形,△PAB与△PAD均是以A为直角顶点的等腰直角三角形,
(1)证明:∵四边形ABCD是正方形,△PAB与△PAD均是以A为直角顶点的等腰直角三角形,
∴PA⊥AD,PA⊥AB,又AD∩AB=A,AB⊥BC,
∴PA⊥平面ABCD,又BC?面ABCD,∴PA⊥BC,
∵AB∩PA=A,∴BC⊥面PAB,
∴BC⊥AF,
∵△PAB是以A为直角顶点的等腰直角三角形,F是PB中点,
∴AF⊥PB,
又PB∩BC=B,∴AF⊥平面PBC,
∵EF?平面PBC,∴AF⊥EF.
(2)解:以A为原点,AD为x轴,AB为y轴,P为z轴,
建立空间直角坐标系,
设AB=1,则A(0,0,0),B(0,1,0),C(1,1,0),P(0,0,1),
$\overrightarrow{AP}$=(0,0,1),$\overrightarrow{AC}$=(1,1,0),
设平面APC的法向量$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{AP}=z=0}\\{\overrightarrow{n}•\overrightarrow{AC}=x+y=0}\end{array}\right.$,取x=1,得$\overrightarrow{n}$=(1,-1,0),
$\overrightarrow{PB}$=(0,1,-1),$\overrightarrow{PC}$=(1,1,-1),
设平面PBC的法向量$\overrightarrow{m}$=(a,b,c),
则$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{PB}=b-c=0}\\{\overrightarrow{m}•\overrightarrow{PC}=a+b-c=0}\end{array}\right.$,取b=1,得$\overrightarrow{m}$=(0,1,1),
|cos<$\overrightarrow{n},\overrightarrow{m}$>|=|$\frac{-1}{\sqrt{2}×\sqrt{2}}$|=$\frac{1}{2}$,
∴<$\overrightarrow{n},\overrightarrow{m}$>=60°,
∴二面角A-PC-B的平面角为60°.
点评 本题考查空间线面关系以及二面角的求解,建立空间坐标系,求出平面的法向量,利用向量法是解决本题的关键.考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力.


 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{5}$ | B. | $\frac{13}{25}$ | C. | $\frac{38}{75}$ | D. | $\frac{81}{125}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥S-ABCD中,底面ABCD是边长为1的菱形,$∠ABC=\frac{π}{4},SA⊥$底面ABCD,SA=2,M为SA的中点.
如图,在四棱锥S-ABCD中,底面ABCD是边长为1的菱形,$∠ABC=\frac{π}{4},SA⊥$底面ABCD,SA=2,M为SA的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
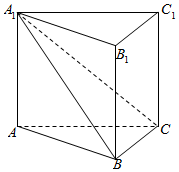 如图,在直三棱柱ABC-A1B1C1中,平面A1BC⊥侧面A1ABB1,且AA1=AB=2
如图,在直三棱柱ABC-A1B1C1中,平面A1BC⊥侧面A1ABB1,且AA1=AB=2查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 9 | B. | $\frac{27}{2}$ | C. | 18 | D. | 27 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
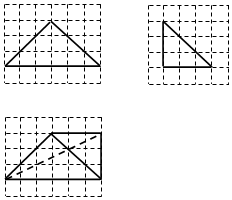
 如图,网格纸上小正方形的边长为1,粗线画出的是某四面体的三视图,则该四面体的表面积为( )
如图,网格纸上小正方形的边长为1,粗线画出的是某四面体的三视图,则该四面体的表面积为( )| A. | 2(1+$\sqrt{2}$+$\sqrt{3}$) | B. | 2(1+2$\sqrt{2}$+$\sqrt{3}$) | C. | 4+2$\sqrt{6}$ | D. | 4(1+$\sqrt{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
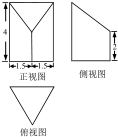 若某几何体的三视图(单位:cm)如图所示,且俯视图为正三角形,则该几何体的体积等于( )
若某几何体的三视图(单位:cm)如图所示,且俯视图为正三角形,则该几何体的体积等于( )| A. | 3$\sqrt{3}$cm3 | B. | 6$\sqrt{3}$cm3 | C. | $\frac{15}{2}\sqrt{3}$cm3 | D. | 9$\sqrt{3}$cm3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,AB⊥平面BCP,CD∥AB,AB=BC=CP=BP=2,CD=1.
如图,在四棱锥P-ABCD中,AB⊥平面BCP,CD∥AB,AB=BC=CP=BP=2,CD=1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com