练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    4．已知函数f（x）=$\frac{a{x}^{2}+1}{bx+c}$（a，b，c∈Z）是奇函数，且f（1）=2，f（2）＜3，则a+b-c=2．

    分析 首先由奇函数定义求c，然后利用f（1）=2，f（2）＜3求a或b的取值范围，最后通过a、b、c∈Z求a、b、c的值，即可得出结论．

    解答 解：由f（-x）=-f（x），得-bx+c=-（bx+c），
    ∴c=0．
    由f（1）=2，得a+1=2b①
    由f（2）＜3，得$\frac{4a+1}{2b}$＜3②
    由①②得$\frac{4a+1}{a+1}$＜3③
    变形可得（a+1）（a-2）＜0，
    解得-1＜a＜2．
    又a∈Z，
    ∴a=0或a=1．
    若a=0，则b=$\frac{1}{2}$，与b∈Z矛盾，
    若a=1，则b=1，
    故a=1，b=1，c=0．
    ∴a+b+c=2，
    故答案为2．

    点评 本题主要考查奇函数的定义，同时考查分式不等式的解法，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    1．命题“在△ABC中，若A＞B，则sinA＞sinB”的逆否命题是（　　）
    A．在△ABC中，若sinA＞sinB，则A＞BB．在△ABC中，若A≤B，则sinA≤sinB
    C．在△ABC中，若sinA＜sinB，则A＜BD．在△ABC中，若sinA≤sinB，则A≤B

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．已知函数f（x）=x2+bx+c，
    （1）若函数f（x）是偶函数，求实数b的值
    （2）若函数f（x）在区间[-1，3]上单调递增，求实数b的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．命题p：?x∈R，cosx＞sinx-1的否定为?x∈R，cosx≤sinx-1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

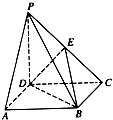    6．如图，在四棱锥P-ABCD中，PD⊥底面ABCD，底面ABCD为矩形，且PD=AD=$\frac{1}{2}$AB，E为PC的中点．
    （1）过点A作一条射线AG，使得AG∥BD，求证：平面PAG∥平面BDE；
    （2）求二面角D-BE-C得余弦值的绝对值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．在直角坐标系xOy中，以坐标原点为极点，x轴极轴建立极坐标系，曲线C1，C2的极坐标方程分别为$2ρsin（θ-\frac{π}{6}）=a（a＞0），ρ=2cosθ$
    （1）求C1的标准方程和C2的参数方程；
    （2）P，Q分别为C1，C2上的动点，若线段PQ长度的最小值为1，求a的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．已知函数f（x）=$\sqrt{（x+1）（x-2）}$与函数g（x）=$\frac{1}{{\sqrt{{x^2}-（2a+1）x+a（a+1）}}}$，若它们的定义域分别为集合A，B，
    （1）求集合A、B；
    （2）若A∩B=A，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．求下列函数的值域：
    （1）f（x）=x2+2x；         
    （2）g（x）=$\frac{1}{x}$，x∈[1，3）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．设数列{an}的前n项和为Sn，且Sn=2n-1，数列{bn}满足b1=2，bn+1-2bn=8an．
    （Ⅰ）求数列{an}、{bn}的通项公式；
    （Ⅱ）设数列{bn}的前n项和为Tn，是否存在常数λ，使得不等式（-1）nλ＜1+$\frac{{T}_{n}-6}{{T}_{n+1}-6}$恒成立？若存在，求出λ的取值范围；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案