
分析 (Ⅰ)利用递推关系即可得出{an}的通项公式,根据bn+1-2bn=8an,可得$\frac{{b}_{n+1}}{{2}^{n+1}}$-$\frac{{b}_{n}}{{2}^{n}}$=2,从而可得{$\frac{{b}_{n}}{{2}^{n}}$}是首项为$\frac{{b}_{1}}{{2}^{1}}$=1,公差为2的等差数列,由此可求{bn}的通项公式;
(Ⅱ)存在常数λ使得不等式(-1)nλ<1+$\frac{{T}_{n}-6}{{T}_{n+1}-6}$(n∈N*)恒成立.利用错位相减法求数列的和,再分类讨论,利用分离参数法,即可得到结论.
解答 (本题满分为13分)
解:(Ⅰ)当n=1时,a1=S1=2-1=1,
当n≥2时,an=Sn-Sn-1=(2n-1)-(2n-1-1)=2n-1,
∵a1=1满足上式,
∴an=2n-1.
∵bn+1-2bn=8an,所以 bn+1-2bn=2n+2,即$\frac{{b}_{n+1}}{{2}^{n+1}}$-$\frac{{b}_{n}}{{2}^{n}}$=2.
∴{$\frac{{b}_{n}}{{2}^{n}}$}是首项为$\frac{{b}_{1}}{{2}^{1}}$=1,公差为2的等差数列.
∴$\frac{{b}_{n}}{{2}^{n}}$=1+2(n-1)=2n-1,
∴bn=(2n-1)•2n
(Ⅱ)存在常数λ使得不等式(-1)nλ<1+$\frac{{T}_{n}-6}{{T}_{n+1}-6}$(n∈N*)恒成立.
因为Tn=1•21+3•22+5•23+…+(2n-3)•2n-1+(2n-1)•2n①
所以2Tn=1•22+3•23+…+(2n-5)•2n-1+(2n-3)•2n+(2n-1)•2n+1②
由①-②得-Tn=2+23+24+…+2n+1-(2n-1)•2n+1,
化简得Tn=(2n-3)•2n+1+6.
因为$\frac{{T}_{n}-6}{{T}_{n+1}-6}$=$\frac{(2n-3)•{2}^{n+1}}{(2n-1)•{2}^{n+2}}$=$\frac{2n-3}{4n-2}$=$\frac{1}{2}$-$\frac{2}{4n-2}$=$\frac{1}{2}-$$\frac{1}{2n-1}$,
(1)当n为奇数时,(-1)λ<1+$\frac{{T}_{n}-6}{{T}_{n+1}-6}$,所以λ>-1-$\frac{{T}_{n}-6}{{T}_{n+1}-6}$,即λ>-$\frac{3}{2}$+$\frac{1}{2n-1}$.
所以当n=1时,-$\frac{3}{2}$+$\frac{1}{2n-1}$的最大值为-$\frac{1}{2}$,所以只需λ>-$\frac{1}{2}$;
(2)当n为偶数时,λ<1+$\frac{{T}_{n}-6}{{T}_{n+1}-6}$,所以λ<$\frac{3}{2}$-$\frac{1}{2n-1}$,
所以当n=2时,$\frac{3}{2}$-$\frac{1}{2n-1}$的最小值为$\frac{7}{6}$,所以只需λ<$\frac{7}{6}$;
由(1)(2)可知存在-$\frac{1}{2}$<λ<$\frac{7}{6}$,使得不等式(-1)nλ<1+$\frac{{T}_{n}-6}{{T}_{n+1}-6}$(n∈N*)恒成立.…(13分)
点评 本题考查了递推关系的意义、等差数列的通项公式,考查了变形能力、推理能力与计算能力,考查存在性问题的探究,考查分离参数法的运用,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
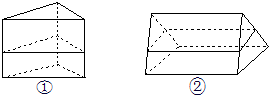 如图①所示一个正三棱柱形容器,高为2,内装水若干,将容器放倒使一个侧面成为底面,这时水面恰为中截面,如图②,则未放倒前的水面高度为1.5.
如图①所示一个正三棱柱形容器,高为2,内装水若干,将容器放倒使一个侧面成为底面,这时水面恰为中截面,如图②,则未放倒前的水面高度为1.5.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,2) | B. | [1,2) | C. | (-∞,2) | D. | (-∞,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,1]∪[1,+∞) | B. | [-1,0] | C. | [0,1] | D. | [-1,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com