
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是正方形,且
是正方形,且![]() ,平面
,平面![]()
![]() 平面
平面![]() ,
,![]() ,点
,点![]() 为线段
为线段![]() 的中点,点
的中点,点![]() 是线段
是线段![]() 上的一个动点.
上的一个动点.
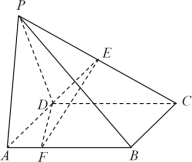
(Ⅰ)求证:平面![]()
![]() 平面
平面![]() ;
;
(Ⅱ)设二面角![]() 的平面角为
的平面角为![]() ,试判断在线段
,试判断在线段![]() 上是否存在这样的点
上是否存在这样的点![]() ,使得
,使得![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(Ⅰ)见证明;(Ⅱ) ![]()
【解析】
(Ⅰ)根据面面垂直的判定定理即可证明结论成立;
(Ⅱ)先证明![]() ,
,![]() ,
,![]() 两两垂直,再以
两两垂直,再以![]() 为原点,以
为原点,以![]() ,
,![]() ,
,![]() 所在直线分别为
所在直线分别为![]() 轴,建立空间直角坐标系,设
轴,建立空间直角坐标系,设![]() ,用
,用![]() 表示出平面
表示出平面![]() 的法向量,进而表示出
的法向量,进而表示出![]() ,由
,由![]() ,即可得出结果.
,即可得出结果.
解:(Ⅰ)![]() 四边形
四边形![]() 是正方形,∴
是正方形,∴![]() .
.
∵平面![]()
![]() 平面
平面![]() 平面
平面![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .
.
∵![]() 平面
平面![]() ,∴
,∴![]() .
.
∵![]() ,点
,点![]() 为线段
为线段![]() 的中点,∴
的中点,∴![]() .
.
又∵![]() ,∴
,∴![]() 平面
平面![]() .
.
又∵![]() 平面
平面![]() ,∴平面
,∴平面![]()
![]() 平面
平面![]() .
.
(Ⅱ)由(Ⅰ)知![]() 平面
平面![]() ,∵
,∵![]() ,∴
,∴![]() 平面
平面![]() .
.
在平面![]() 内过
内过![]() 作
作![]() 交
交![]() 于点
于点![]() ,
,
∴![]() ,故
,故![]() ,
,![]() ,
,![]() 两两垂直,以
两两垂直,以![]() 为原点,
为原点,
以![]() ,
,![]() ,
,![]() 所在直线分别为
所在直线分别为![]() 轴,建立如图所示空间直角坐标系
轴,建立如图所示空间直角坐标系![]() .
.
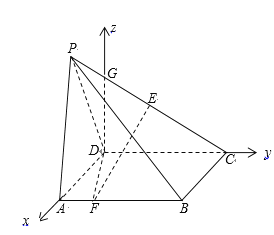
因为![]() ,
,![]() ,∴
,∴![]() .
.
∵![]() 平面
平面![]() , 则
, 则![]() ,
,![]() ,
,![]()
又![]() 为
为![]() 的中点,
的中点,![]() ,
,
假设在线段![]() 上存在这样的点
上存在这样的点![]() ,使得
,使得![]() ,设
,设![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的法向量为
的法向量为![]() , 则
, 则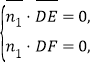
∴ ,令
,令![]() ,则
,则![]() ,则
,则![]()
![]()
![]() 平面
平面![]() ,
,![]() 平面
平面![]() 的一个法向量
的一个法向量![]() ,
,![]() ,则
,则![]()
∴![]() .
.
![]() ,解得
,解得![]() ,∴
,∴![]()


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案科目:高中数学 来源: 题型:
【题目】甲乙两名射击运动员分别对一目标射击一次,甲射中的概率为0.8,乙射中的概率为0.9,求:
(1)2人都射中目标的概率;
(2)2人中恰有1人射中目标的概率;
(3)2人至少有1人射中目标的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=loga(x+1)-loga(1-x),a>0且a≠1.
(1)求f(x)的定义域;
(2)判断f(x)的奇偶性并予以证明;
(3)当a>1时,求使f(x)>0的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.某班![]() 位同学从文学、经济和科技三类不同的图书中任选一类,不同的结果共有
位同学从文学、经济和科技三类不同的图书中任选一类,不同的结果共有![]() 种;
种;
B.甲乙两人独立地解题,已知各人能解出的概率分别是![]() ,则题被解出的概率是
,则题被解出的概率是![]() ;
;
C.某校![]() 名教师的职称分布情况如下:高级占比
名教师的职称分布情况如下:高级占比![]() ,中级占比
,中级占比![]() ,初级占比
,初级占比![]() ,现从中抽取
,现从中抽取![]() 名教师做样本,若采用分层抽样方法,则高级教师应抽取
名教师做样本,若采用分层抽样方法,则高级教师应抽取![]() 人;
人;
D.两位男生和两位女生随机排成一列,则两位女生不相邻的概率是![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com