
分析 (Ⅰ)从中随机抽取1个小球,取到黑色小球的概率是$\frac{1}{3}$,列出方程.求解n的值;
(Ⅱ)(ⅰ)求出从袋子中现从袋子中有放回地随机抽取2个小球的所有事件个数,满足“a+b=2”为事件A的个数,然后求解概率;
(ⅱ)直接利用几何概型,求解全部结果的区域面积与所求结果的区域面积,求解概率即可.
解答 解:(Ⅰ)依题意$\frac{n}{n+2}=\frac{1}{3}$,得n=1
(Ⅱ)(ⅰ)记标号为0的小球为s,标号为1的小球为t,标号为2的小球为k,
则取出2个小球的可能情况有:(s,t),(s,k),(t,s),(t,k),(k,s),(k,t),(s,s),(t,t),(k,k),共9种,
其中满足“a+b=2”的有3种:(s,k),(k,s)(t,t).
所以所求概率为$P(A)=\frac{1}{3}$
(ⅱ)记“x2+y2>(a-b)2恒成立”为事件B.
则事件B等价于“x2+y2>4恒成立”,(x,y)可以看成平面中的点的坐标,则全部结果所构成的区域为Ω={(x,y)|0≤x≤2,0≤y≤2,x,y∈R},
而事件B构成的区域为B={(x,y)|x2+y2>4,(x,y)∈Ω}.
所以所求的概率为P(B)=$\frac{S_B}{S_Ω}$=1-$\frac{π}{4}$.
点评 本题考查古典概型以及几何概型的概率的求法,基本知识的考查,属于中档题.


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 相离 | B. | 相切 | C. | 相交 | D. | 随m的变化而变化 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,π) | B. | (0,π] | C. | (0,4π) | D. | (0,4π] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
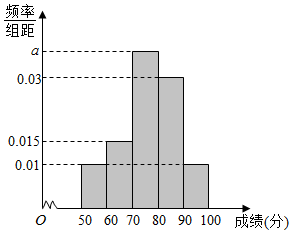 100名学生某次数学考试成绩(单位:分)的频率分布直方图如图所示.
100名学生某次数学考试成绩(单位:分)的频率分布直方图如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{{\sqrt{3}}}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com