Question

4．长方体AC₁的长、宽、高分别为3、2、1，求从A到C₁沿长方体的表面的最短距离．

Answer 1

分析 画出长方体的侧面展开图，然后求其三角形的边长AC₁的长，

解答 解：结合长方体的三种展开图不难求得AC₁的长分别是：
（1）将侧面ABB₁A₁和底面A₁B₁C₁D₁展开，则有$A{C_1}=\sqrt{{3^2}+{3^2}}=3\sqrt{2}$，即经过侧面ABB₁A₁和底面A₁B₁C₁D₁时的最短距离是$3\sqrt{2}$；
（2）将侧面ABB₁A₁和面BB₁C₁C展开，则有AC₁=$\sqrt{25+1}$=$\sqrt{26}$，即经过侧面ABB₁A₁和面BB₁C₁C时的最短距离是$\sqrt{26}$；
（3）将侧面ADD₁A₁和底面A₁B₁C₁D₁展开，则有$A{C_1}=\sqrt{{4^2}+{2^2}}=2\sqrt{5}$，
即经过侧面ADD₁A₁和底面A₁B₁C₁D₁时的最短距离是$2\sqrt{5}$．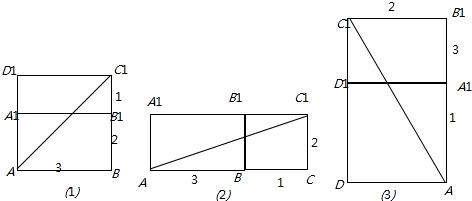

由于$3\sqrt{2}＜2\sqrt{5}$，$3\sqrt{2}＜2\sqrt{6}$，所以由A到C₁的正方体表面上的最短距离为$3\sqrt{2}$．

点评 求表面上最短距离常把图形展成平面图形．考查学生几何体的展开图，空间想象能力，是中档题．