
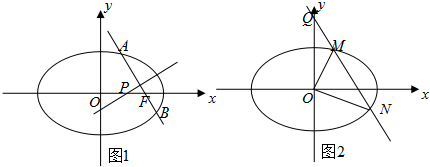
分析 (1)直接由已知得到a,b的值,则椭圆方程可求;
(2)联立直线方程和椭圆方程,利用根与系数的关系求出A、B中点的坐标,得到l1的垂直平分线的方程,求得P的坐标,进一步求出|PF|、|AB|得答案;
(3)联立直线方程和椭圆方程,把△OMQ与△ONQ面积之比转化为M、N的横坐标的比值得答案.
解答 解:(1)由题意得$\left\{\begin{array}{l}{a=2}\\{b=1}\end{array}\right.$,∴椭圆C1的方程为$\frac{x2}{4}$+y2=1;
(2)设A(x1,y1),B(x2,y2),中点D(x0,y0).设直线l1的方程为x=my+$\sqrt{3}$.($-\sqrt{3}<m<\sqrt{3}$),
由$\left\{\begin{array}{l}{x=my+\sqrt{3}}\\{{x}^{2}+4{y}^{2}=4}\end{array}\right.$,消去x整理得$({m}^{2}+4){y}^{2}+2\sqrt{3}y-1=0$,
则${y}_{0}=\frac{{y}_{1}+{y}_{2}}{2}=-\frac{\sqrt{3}m}{{m}^{2}+4}$,${x}_{0}=m{y}_{0}+\sqrt{3}=\frac{4\sqrt{3}}{{m}^{2}+4}$.
∴l1的垂直平分线的方程为:y-y0=-m(x-x0),即$y+\frac{\sqrt{3}m}{{m}^{2}+4}=-m(x-\frac{4\sqrt{3}}{{m}^{2}+4})$,
令y=0,得$x=\frac{3\sqrt{3}}{{m}^{2}+4}$.即P($\frac{3\sqrt{3}}{{m}^{2}+4},0$).
∴|PF|=$\sqrt{3}-\frac{3\sqrt{3}}{{m}^{2}+4}=\frac{\sqrt{3}({m}^{2}+1)}{{m}^{2}+4}$,
又|AB|=|AF|+|BF|=$\frac{4({m}^{2}+1)}{{m}^{2}+4}$,
∴$\frac{|PF|}{|AB|}$=$\frac{\sqrt{3}}{4}$;
(3)设直线l2的方程为y=kx+2,由$\left\{\begin{array}{l}{y=kx+2}\\{{x}^{2}+4{y}^{2}=4}\end{array}\right.$消去y,得(4k2+1)x2+16kx+12=0.
则△=256k2-48(4k2+1)>0,得${k}^{2}>\frac{3}{4}$.
设M(x1,y1),N(x2,y2),则$\frac{{S}_{△OMQ}}{{S}_{△ONQ}}=\frac{|MQ|}{|NQ|}=\frac{{x}_{1}}{{x}_{2}}$,由题意,0<$\frac{{x}_{1}}{{x}_{2}}$<1.
又${x}_{1}+{x}_{2}=\frac{-16k}{4{k}^{2}+1},{x}_{1}{x}_{2}=\frac{12}{4{k}^{2}+1}$,
则$\frac{({x}_{1}+{x}_{2})^{2}}{{x}_{1}{x}_{2}}=\frac{{x}_{1}}{{x}_{2}}+\frac{{x}_{2}}{{x}_{1}}+2$=$\frac{\frac{256{k}^{2}}{(4{k}^{2}+1)^{2}}}{\frac{12}{4{k}^{2}+1}}=\frac{64{k}^{2}}{12{k}^{2}+3}$,
∵${k}^{2}>\frac{3}{4}$,∴$\frac{64{k}^{2}}{12{k}^{2}+3}$∈(4,$\frac{16}{3}$),∴2<$\frac{{x}_{1}}{{x}_{2}}+\frac{{x}_{2}}{{x}_{1}}$<$\frac{10}{3}$.
∴$\frac{{x}_{1}}{{x}_{2}}$∈($\frac{5-\sqrt{22}}{3},1$),
即$\frac{{S}_{△OMQ}}{{S}_{△ONQ}}$∈($\frac{5-\sqrt{22}}{3},1$).
点评 本题考查椭圆的简单性质,考查了直线与圆锥曲线位置关系的应用,考查了运算能力,是压轴题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图所示,边长为3的正方形中有一封闭曲线围成的阴影区域,在正方形中随机的撒一粒豆子,它落在阴影区域内的概率为$\frac{1}{3}$,则阴影区域的面积为3.
如图所示,边长为3的正方形中有一封闭曲线围成的阴影区域,在正方形中随机的撒一粒豆子,它落在阴影区域内的概率为$\frac{1}{3}$,则阴影区域的面积为3.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com