
分析 (Ⅰ)先解绝对值不等式,再根据集合之间的关系即可求出a的范围
(Ⅱ)化简|f(x)-f(a)|为|x-a||x+a-1|,小于|x+a-1|即|(x-a)+(2a-1)|.再由|(x-a)+(2a-1)|≤|x-a|+|2a-1|<1+2|a|+1,从而证得结论.
解答 解:(Ⅰ)∵|x-a|<1,
∴a-1<x<a+1,
∵x∈(-1,1),不等式|x-a|<1恒成立,
∴$\left\{\begin{array}{l}{a-1≥-1}\\{a+1≤1}\end{array}\right.$,
解得a=0,
∴实数a的取值范围构成的集合{0}
(Ⅱ)证明:∵函数f(x)=x2-x+c,实数a满足|x-a|<1,
∴|f(x)-f(a)|=|x2-x+c-(a2-a+c)|=|x-a||x+a-1|<|x+a-1|
=|(x-a)+(2a-1)|≤|x-a|+|2a-1|<1+2|a|+1=2(|a|+1),
即|f(x)-f(a)|<2(|a|+1)成立.
点评 本题主要考查绝对值不等式的性质的应用以及不等式恒成立的问题,属于中档题.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 若a,b,c∈R,则“ax2+bx+c≥0”的充分条件是“b2-4ac≤0” | |
| B. | 若a,b,c∈R,则“ab2≥cb2”的充要条件是“a>c” | |
| C. | 命题“对任意x∈R,有x2≥0”的否定是“存在x∈R,有x2≥0” | |
| D. | 命题“l是一条直线,α,β是两个不同的平面,若l∥α,l∥β,则α∥β”为假命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
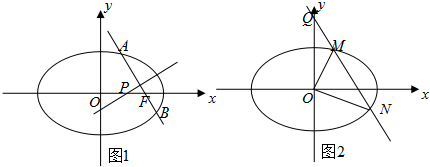
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{5}{4}$ | C. | $\frac{5}{4}$或2 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $?{x_0}∈R,x_0^2+{x_0}≥1$ | B. | ?x∈R,x2+x≥1 | ||
| C. | $?{x_0}∈R,x_0^2+{x_0}>1$ | D. | ?x∈R,x2+x>1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com