
分析 S(a,b)=1-$\frac{ab(1-ab)}{(1+a)(1+b)}$,令T=$\frac{ab(1-ab)}{(1+a)(1+b)}$,X=$\sqrt{ab}$,则T=f(X)=$\frac{{x}^{2}(1-X)}{1+x}$,X∈[0,1],利用导数法,求出函数的最值,可得答案.
解答 解:∵a,b∈[0,1],
∴S(a,b)=$\frac{a}{1+b}$+$\frac{b}{1+a}$+(1-a)(1-b)=1-$\frac{ab(1-ab)}{(1+a)(1+b)}$,
令T=$\frac{ab(1-ab)}{(1+a)(1+b)}$,X=$\sqrt{ab}$,
则T=$\frac{ab(1-ab)}{(1+a)(1+b)}$=$\frac{ab(1-ab)}{1+a+b+ab}$<$\frac{ab(1-ab)}{1+2\sqrt{ab}+ab}$=$\frac{{X}^{2}(1-{X}^{2})}{(1+X)^{2}}$=$\frac{{x}^{2}(1-X)}{1+x}$,
令f(X)=$\frac{{x}^{2}(1-X)}{1+x}$,X∈[0,1],
可得:f′(X)=$\frac{{-2X}^{\;}({X}^{2}+X-1)}{{(1+X)}^{2}}$,X∈[0,1],
X∈[0,$\frac{\sqrt{5}-1}{2}$)时,f′(X)>0,
X∈($\frac{\sqrt{5}-1}{2}$,1]时,f′(X)<0,
故当X=$\frac{\sqrt{5}-1}{2}$时,f(X)取最大值$\frac{5\sqrt{5}-11}{2}$,
故S(a,b)=$\frac{a}{1+b}$+$\frac{b}{1+a}$+(1-a)(1-b)的最小值为1-$\frac{5\sqrt{5}-11}{2}$=$\frac{13-5\sqrt{5}}{2}$,
故答案为:$\frac{13-5\sqrt{5}}{2}$
点评 本题考查的知识点是导数在求函数最值中的应用,构造法,转化思想,函数的最值及其几何意义,难度较大.


科目:高中数学 来源: 题型:解答题
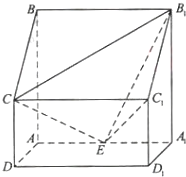 如图,四棱柱ABCD-A1B1C1D1中,侧棱A1A⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,AA1=AB=2,E为棱AA1的中点.
如图,四棱柱ABCD-A1B1C1D1中,侧棱A1A⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,AA1=AB=2,E为棱AA1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
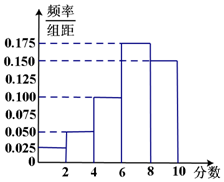 某汽车公司为了考查某4S店的服务态度,对到店维修保养的客户进行回访调查,每个用户在到此店维修或保养后可以对该店进行打分,最高分为10分.上个月公司对该4S店的100位到店维修保养的客户进行了调查,将打分的客户按所打分值分成以下几组:
某汽车公司为了考查某4S店的服务态度,对到店维修保养的客户进行回访调查,每个用户在到此店维修或保养后可以对该店进行打分,最高分为10分.上个月公司对该4S店的100位到店维修保养的客户进行了调查,将打分的客户按所打分值分成以下几组:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com