
 某汽车公司为了考查某4S店的服务态度,对到店维修保养的客户进行回访调查,每个用户在到此店维修或保养后可以对该店进行打分,最高分为10分.上个月公司对该4S店的100位到店维修保养的客户进行了调查,将打分的客户按所打分值分成以下几组:
某汽车公司为了考查某4S店的服务态度,对到店维修保养的客户进行回访调查,每个用户在到此店维修或保养后可以对该店进行打分,最高分为10分.上个月公司对该4S店的100位到店维修保养的客户进行了调查,将打分的客户按所打分值分成以下几组:分析 (Ⅰ)根据已知中频率分布直方图,求出打分值在[6,10]的频率,进而可得打分值在[6,10]的客户的人数:
(II)求出从这6人中随机抽取2人的情况总数,及两人来自不同组的情况数,代入概率公式,可得答案.
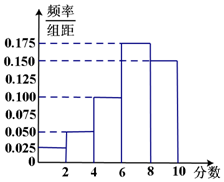
解答 解:(Ⅰ)由直方图知,所打分值在[6,10]的频率为(0.175+0.150)×2=0.65.
所以所打分值在[6,10]的客户的人数 为0.65×100=65 人.…(4分)
(Ⅱ)由直方图知,第二、三组客户人数分别为10人和20人,所以抽出的6人中,第二组有2人,设为A,B;第三组有4人,设为a,b,c,d.
从中随机抽取2人的所有情况如下:
AB,Aa,Ab,Ac,Ad,Ba,Bb,Bc,Bd,ab,ac,ad,bc,bd,cd共15种.…(8分)
其中,两人来自不同组的情况有:Aa,Ab,Ac,Ad,Ba,Bb,Bc,Bd共有8种,…(10分)
所以,得到奖励的人来自不同组的概率为$\frac{8}{15}$.…(12分)
点评 本题考查的知识点是频率分布直方图,古典概型,难度不大,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $?{x_0}∈R,x_0^2+{x_0}≥1$ | B. | ?x∈R,x2+x≥1 | ||
| C. | $?{x_0}∈R,x_0^2+{x_0}>1$ | D. | ?x∈R,x2+x>1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{4}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{3π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com