
分析 (1)求出函数的导数,解关于导函数的方程,求出函数的单调区间即可;(2)通过讨论a的范围,求出函数的最小值即可.
解答 解:(1)f′(x)=$\frac{(2x+3a)(x-a)}{x}$,(x>0),
令f′(x)=0,解得:x1=a,x2=-$\frac{3a}{2}$(舍),
x,f′(x),f(x)的变化如下:
| x | (0,a) | a | (a,+∞) |
| f′(x) | - | 0 | + |
| f(x) | 递减 | 极小值 | 递增 |
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想,是一道中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
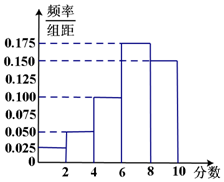 某汽车公司为了考查某4S店的服务态度,对到店维修保养的客户进行回访调查,每个用户在到此店维修或保养后可以对该店进行打分,最高分为10分.上个月公司对该4S店的100位到店维修保养的客户进行了调查,将打分的客户按所打分值分成以下几组:
某汽车公司为了考查某4S店的服务态度,对到店维修保养的客户进行回访调查,每个用户在到此店维修或保养后可以对该店进行打分,最高分为10分.上个月公司对该4S店的100位到店维修保养的客户进行了调查,将打分的客户按所打分值分成以下几组:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}+\frac{{\sqrt{3}}}{4}$ | B. | $\frac{1}{2}-\frac{{\sqrt{3}}}{4}$ | C. | $\frac{3}{4}$ | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(sinα)>f(cosβ) | B. | f(sinα)>f(sinβ) | C. | f(sinα)<f(cosβ) | D. | f(cosα)>f(cosβ) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com