
分析 (1)利用等差数列的通项公式及其前n项和公式即可得出.
(2)利用等比数列的通项公式及其前n项和公式即可得出.
解答 解:(1)∵等差数列{an}中,a1=$\frac{3}{2}$,d=-$\frac{1}{2}$,
∴an=a1+(n-1)d=$\frac{3}{2}$-$\frac{1}{2}$n+$\frac{1}{2}$=2-$\frac{n}{2}$.
∵Sn=-15,
∴$\frac{n(\frac{3}{2}+2-\frac{n}{2})}{2}$=-15,
解得n=12或n=-5(舍去).
综上所述,n=12,an=2-$\frac{n}{2}$.
(2))∵Sn=189,q=2,an=96,
∴$\left\{\begin{array}{l}{\frac{{a}_{1}({2}^{n}-1)}{2-1}=189}\\{{a}_{1}{2}^{n-1}=96}\end{array}\right.$,
解得a1=3,n=6.
点评 本题考查了等差数列和等比数列的通项公式及其前n项和公式,属于基础题.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x=0 | B. | x=$\frac{π}{6}$ | C. | x=-$\frac{π}{12}$ | D. | x=$\frac{π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
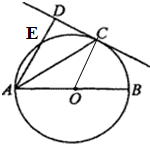 如图,已知AB是圆O的直径,直线CD与圆O相切于点C,AC平分∠DAB,AD与圆O相交于点E
如图,已知AB是圆O的直径,直线CD与圆O相切于点C,AC平分∠DAB,AD与圆O相交于点E查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com