Question

9．一半径为6米的水轮如图，水轮圆心O距离水面3米，已知水轮每分钟转动4圈，水轮上点P从水中浮现时开始到其第一次达到最高点的用时为5秒．

Answer 1

分析 由已知可得水轮上点P从水中浮现时开始到其第一次达到最高点要旋转120°，即$\frac{1}{3}$个周期，进而根据水轮每分钟转动4圈，求出周期，可得答案．

解答 解：过O作水平的垂线，垂足为Q，如下图所示：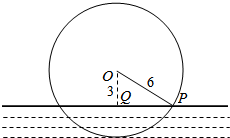

由已知可得：OQ=3，OP=6，
则cos∠POQ=$\frac{1}{2}$，即∠POQ=60°，
则水轮上点P从水中浮现时开始到其第一次达到最高点要旋转120°，即$\frac{1}{3}$个周期，
又由水轮每分钟转动4圈，可知周期是15秒，
故水轮上点P从水中浮现时开始到其第一次达到最高点的用时为5秒，
故答案为：5

点评 本题考查的知识点是三角函数的周期，在实际问题中建立三角函数模型的问题．难度不大，属于基础题．