
分析 设P(x0,y0)为圆C上的任意一点,在矩阵A对应的变换下变为另一个点P'(x'0,y'0),代入椭圆方程,对照圆的方程即可求出a和b的值;
解答 解:设P(x0,y0)为圆C上的任意一点,在矩阵A对应的变换下变为另一个点P'(x'0,y'0),
则 $[\begin{array}{l}{{x'}_0}\\{{y'}_0}\end{array}]=[\begin{array}{l}a\;\;0\\ 0\;\;b\end{array}][\begin{array}{l}{x_0}\\{y_0}\end{array}]$,…2分$\left\{\begin{array}{l}{{x'}_0}=a\;{x_0}\\{{y'}_0}=b\;{y_0}\end{array}\right.$所以 $\left\{\begin{array}{l}{x_0}=\frac{{{{x'}_0}}}{a}\\{y_0}=\frac{{{{y'}_0}}}{b}\end{array}\right.$…4分
又因为点P(x0,y0)在圆C:x2+y2=1上,所以 ${x^2}_0+{y_0}^2=1$,…6分
所以 $\frac{x'_0^2}{a^2}+\frac{y'_0^2}{b^2}=1$,即 $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$.
由已知条件可知,椭圆方程为${x^2}+\frac{y^2}{4}=1$,…8分
所以 a2=1,b2=4,因为 a>0,b>0,
所以 a=1,b=2. …10分.
点评 本题主要考查了特殊矩阵的变换,同时考查了计算能力,属于基础题.


科目:高中数学 来源: 题型:解答题
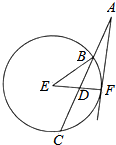 如图,过圆E外一点A作一条直线与圆E交B,C两点,且AB=$\frac{1}{3}$AC,作直线AF与圆E相切于点F,连接EF交BC于点D,己知圆E的半径为2,∠EBC=$\frac{π}{6}$.
如图,过圆E外一点A作一条直线与圆E交B,C两点,且AB=$\frac{1}{3}$AC,作直线AF与圆E相切于点F,连接EF交BC于点D,己知圆E的半径为2,∠EBC=$\frac{π}{6}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| a | b | c | d | e | f | g | h | i | j | k | l | m |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| n | o | p | q | r | s | t | u | v | w | x | y | z |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com