
分析 通过对an=$\frac{{a}_{n-1}}{1+{a}_{n-1}}$(n≥2)两边同时取倒数可知$\frac{1}{{a}_{n}}$=$\frac{1}{{a}_{n-1}}$+1,进而可知数列{$\frac{1}{{a}_{n}}$}是以$\frac{1}{2}$为首项、1为公差的等差数列,计算即得结论.
解答 解:∵an=$\frac{{a}_{n-1}}{1+{a}_{n-1}}$(n≥2),
∴$\frac{1}{{a}_{n}}$=$\frac{1+{a}_{n-1}}{{a}_{n-1}}$=$\frac{1}{{a}_{n-1}}$+1,
又∵$\frac{1}{{a}_{1}}$=$\frac{1}{2}$,
∴数列{$\frac{1}{{a}_{n}}$}是以$\frac{1}{2}$为首项、1为公差的等差数列,
∴$\frac{1}{{a}_{n}}$=$\frac{1}{2}$+(n-1)=$\frac{2n-1}{2}$,
∴an=$\frac{2}{2n-1}$.
点评 本题考查数列的通项,对表达式的灵活变形是解决本题的关键,注意解题方法的积累,属于中档题.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:选择题
| A. | -200 | B. | -100 | C. | 200 | D. | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
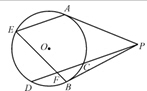 过圆O外一点P向圆引两条切线PA、PB和割线PCD,从A点作弦AE平行于CD,连接BE交CD于F.
过圆O外一点P向圆引两条切线PA、PB和割线PCD,从A点作弦AE平行于CD,连接BE交CD于F.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 32014 | B. | 32014-1 | C. | 32015 | D. | 32015-1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com