
分析 (Ⅰ)根据余弦定理求出BD,再根据三角形的面积公式计算即可,
(Ⅱ)根据正弦定理即可求出sin∠BDC=sin(C+45°)=$\frac{2\sqrt{5}}{5}$,再由正弦定理可得答案.
解答 解:(Ⅰ)在△BCD中,由余弦定理:CD2=BC2+BD2-2BC•BD•cos45°,
即20=8+BD2-4BD,
解得BD=6,
所以S△BCD=$\frac{1}{2}$•BD•BC•sin45°=$\frac{1}{2}$×6×2$\sqrt{2}$×$\frac{\sqrt{2}}{2}$=6
(Ⅱ)由正弦定理可得:$\frac{BC}{sinA}$=$\frac{AB}{sinC}$,即$\frac{2\sqrt{2}}{\frac{\sqrt{10}}{10}}$=$\frac{6\sqrt{2}}{sinC}$,
解得sinC=$\frac{3\sqrt{10}}{10}$,
由角C为锐角得cosC=$\frac{\sqrt{10}}{10}$,
∴sin∠BDC=sin(C+45°)=$\frac{2\sqrt{5}}{5}$,
在△BCD中,由正弦定理得:$\frac{CD}{sin∠DBC}$=$\frac{BC}{sin∠BDC}$,
即$\frac{CD}{\frac{\sqrt{2}}{2}}$=$\frac{2\sqrt{2}}{\frac{2\sqrt{5}}{5}}$,
解得CD=$\sqrt{5}$.
点评 本题考查了正弦定理和余弦定理和三角形的面积公式,考查了学生的运算能力,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
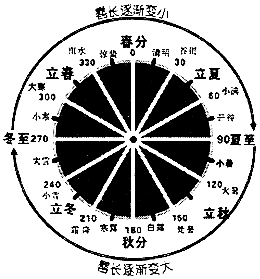 我国古代的天文学和数学著作《周髀算经》中记载:一年有二十四个节气,每个节气晷(guǐ)长损益相同(晷是按照日影测定时刻的仪器,晷长即为所测量影子的长度).二十四节气及晷长变化如图所示,相邻两个节气晷长的变化量相同,周而复始.若冬至晷长一丈三尺五寸,夏至晷长一尺五寸(一丈等于十尺,一尺等于十寸),则夏至之后的那个节气(小暑)晷长是( )
我国古代的天文学和数学著作《周髀算经》中记载:一年有二十四个节气,每个节气晷(guǐ)长损益相同(晷是按照日影测定时刻的仪器,晷长即为所测量影子的长度).二十四节气及晷长变化如图所示,相邻两个节气晷长的变化量相同,周而复始.若冬至晷长一丈三尺五寸,夏至晷长一尺五寸(一丈等于十尺,一尺等于十寸),则夏至之后的那个节气(小暑)晷长是( )| A. | 五寸 | B. | 二尺五寸 | C. | 三尺五寸 | D. | 四尺五寸 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-2,0] | B. | [-2,0)∪[2,+∞) | C. | [-2,0) | D. | (-∞,0)∪[2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com