
【题目】近年来我国电子商务行业迎来蓬勃发展的新机遇相关管理部门推出了针对电商的商品和服务的评价体系.现从评价系统中选出![]() 次成功交易,并对其评价进行统计爱,商品和服务评价的
次成功交易,并对其评价进行统计爱,商品和服务评价的![]() 列联表如下表:
列联表如下表:
对服务好评 | 对服务不满意 | 合计 | |
对商品好评 |
|
|
|
对商品不满意 |
|
|
|
合计 |
|
|
|
(1)是否可以在犯错误概率不超过![]() 的前提下,认为商品好评与服务好评有关?
的前提下,认为商品好评与服务好评有关?
(2)若将频率视为概率,某人在该购物平台上进行的![]() 次购物中,设对商品和服务全好评的次数为随机变量
次购物中,设对商品和服务全好评的次数为随机变量![]() ,求
,求![]() 的数学期望.
的数学期望.
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(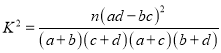 ,其中
,其中![]() )
)
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:高中数学 来源: 题型:
【题目】已知直线C1:  ( t 为参数),曲线C2:
( t 为参数),曲线C2: ![]() (r>0,θ为参数).
(r>0,θ为参数).
(1)当r=1时,求C 1 与C2的交点坐标;
(2)点P 为曲线 C2上一动点,当r=![]() 时,求点P 到直线C1距离最大时点P 的坐标.
时,求点P 到直线C1距离最大时点P 的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD与BDEF均为菱形,∠DAB=∠DBF=60°,且FA=FC.
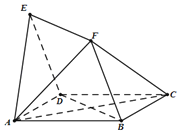
(Ⅰ)求证:AC⊥平面BDEF;
(Ⅱ)求证:FC∥平面EAD;
(Ⅲ)求二面角A﹣FC﹣B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某险种的基本保费为![]() (单位:元),继续购买该险种的投保人称为续保人,
(单位:元),继续购买该险种的投保人称为续保人,
续保人本年度的保费与其上年度出险次数的关联如下:
上年度出险次数 | 0 | 1 | 2 | 3 | 4 |
|
保费 |
|
|
|
|
|
|
随机调查了该险种的400名续保人在一年内的出险情况,得到如下统计表:
出险次数 | 0 | 1 | 2 | 3 | 4 |
|
频数 | 120 | 100 | 60 | 60 | 40 | 20 |
(Ⅰ)记A为事件:“一续保人本年度的保费不高于基本保费”.求![]() 的估计值;
的估计值;
(Ⅱ)记B为事件:“一续保人本年度的保费高于基本保费但不高于基本保费的190%”.
求![]() 的估计值;
的估计值;
(III)求续保人本年度的平均保费估计值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一种计算装置,有一数据入口A和一个运算出口B,按照某种运算程序:①当从A口输入自然数1时,从B口得到 ![]() ,记为
,记为 ![]() ;②当从A口输入自然数n(n≥2)时,在B口得到的结果f(n)是前一个结果f(n﹣1)的
;②当从A口输入自然数n(n≥2)时,在B口得到的结果f(n)是前一个结果f(n﹣1)的 ![]() 倍. (Ⅰ)当从A口分别输入自然数2,3,4时,从B口分别得到什么数?
倍. (Ⅰ)当从A口分别输入自然数2,3,4时,从B口分别得到什么数?
(Ⅱ)根据(Ⅰ)试猜想f(n)的关系式,并用数学归纳法证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列各组函数中,表示同一个函数的是( )
A.y= ![]() 与y=x+1
与y=x+1
B.y=lgx与y= ![]() lgx2
lgx2
C.y= ![]() ﹣1与y=x﹣1
﹣1与y=x﹣1
D.y=x与y=logaax(a>0且a≠1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C1的参数方程为 ![]() (t为参数),以原点O为极点,以x轴正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=﹣
(t为参数),以原点O为极点,以x轴正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=﹣ ![]() .
.
(1)求曲线C1的普通方程与曲线C2的直角坐标方程;
(2)若C1上的点P对应的参数为t= ![]() ,Q为C2上的动点,求PQ中点M到直线C3:
,Q为C2上的动点,求PQ中点M到直线C3: ![]() (α为参数)距离的最小值.
(α为参数)距离的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com