
| A. | ${\vec e}_1={\vec e}_2$ | B. | ${\vec e}_1∥{\vec e}_2$ | C. | $|{{\vec e}_1}|=|{{\vec e}_2}|$ | D. | 以上都不对 |
分析 根据${\vec e}_1,{\vec e}_2$是两个单位向量即得到:|$\overrightarrow{{e}_{1}}$|=|$\overrightarrow{{e}_{2}}$|=1,进而得到正确选项.
解答 解:∴${\vec e}_1,{\vec e}_2$是两个单位向量,
则|$\overrightarrow{{e}_{1}}$|=1,|$\overrightarrow{{e}_{2}}$|=1,
∴|$\overrightarrow{{e}_{1}}$|=|$\overrightarrow{{e}_{2}}$|,
故选:C.
点评 本题考查了单位向量的概念,属于概念考查题,应该掌握.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{8}{3}$ | B. | $\frac{32}{3}$π | C. | $\frac{8}{3}$π | D. | 24π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
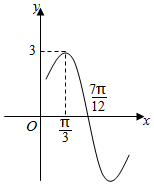 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,-π<φ<0).
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,-π<φ<0).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 120 | B. | 114 | C. | 105 | D. | 75 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com