练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设p：实数x满足x2－4ax＋3a2<0，其中a≠0，q：实数x满足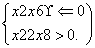

    (1)若a＝1，且p∧q为真，求实数x的取值范围；

    (2)若p是q的必要不充分条件，求实数a的取值范围．


    解：(1)由x2－4ax＋3a2<0，得(x－3a)(x－a)<0，

    当a＝1时，解得1<x<3，即p为真时实数x的取值范围是1<x<3.

    由，得2<x≤3，即q为真时实数x的取值范围是2<x≤3.

    若p∧q为真，则p真且q真，所以实数x的取值范围是2<x<3.

    (2)p是q的必要不充分条件，即q⇒p且pq，设A＝{x|p(x)}，B＝{x|q(x)}，则AB，

    又B＝(2,3]，当a>0时，A＝(a,3a)；

    a<0时，A＝(3a，a)．

    所以当a>0时，有解得1<a≤2；

    当a<0时，显然A∩B＝∅，不合题意．

    综上所述，实数a的取值范围是1<a≤2.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知椭圆上的一点到椭圆一个焦点的距离为，则到另一焦点距离为                                                                （   ）

    A   　　　　 B    　　　　 C   　　　　　　 D

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知集合A＝{(x，y)|x，y是实数，且x2＋y2＝1}，B＝{(x，y)|x，y是实数，且y＝x}，则A∩B的元素个数为(　　)．

    A．0            B．1            C．2            D．3

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知α，β角的终边均在第一象限，则“α＞β”是“sin α＞sin β”的(　　)．

    A．充分不必要条件                                  B．必要不充分条件

    C．充要条件                                        D．既不充分也不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    p：“向量a与向量b的夹角θ为锐角”是q：“a·b>0”的________条件．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     “”的含义为（）

    A．不全为0                      

    B． 全不为0            

    C．至少有一个为0               

    D．不为0且为0，或不为0且为0

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知命题“∀x∈R，x2－5x＋a＞0”的否定为假命题，则实数a的取值范围是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    记f(x)＝lg(2x－3)的定义域为集合M，函数g(x)＝ 的定义域为集合N，求：

    (1)集合M、N；

    (2)集合M∩N，M∪N.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    函数f(x)＝ax2＋bx＋c(a≠0)的图象关于直线x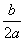＝－对称．据此可推测，对任意的非零实数a，b，c，m，n，p，关于x的方程m[f(x)]2＋nf(x)＋p＝0的解集都不可能是(　　)．

    A．{1,2}                            B．{1,4}

    C．{1,2,3,4}                        D．{1,4,16,64}

    查看答案和解析>>

    同步练习册答案