
分析 (1)首先对f(x)求导,求出(1,f(1))点处的切线方程与3x-y-2=0相等即可;
(2)由题意转换为:令$g(x)=\frac{xlnx+2x-1}{x-1}$,则k<g(x)min.利用导数求出g(x)的最小值即可.
解答 解:(1)f(x)的定义域为(0,+∞),f'(x)=lnx+1+a,
∴$\left\{\begin{array}{l}f'(1)=a+1=3\\ f(1)=a+b=1\end{array}\right.$⇒$\left\{\begin{array}{l}a=2\\ b=-1\end{array}\right.$
∴f(x)=xlnx+2x-1.
(2)$k<\frac{f(x)}{x-1}$可化为$k<\frac{xlnx+2x-1}{x-1}$,
令$g(x)=\frac{xlnx+2x-1}{x-1}$,则k<g(x)min,$g'(x)=\frac{x-2-lnx}{{{{(x-1)}^2}}}$,x∈(1,+∞).
令h(x)=x-2-lnx,
则$h'(x)=1-\frac{1}{x}=\frac{x-1}{x}>0$,
∴h(x)在(1,+∞)上为增函数.
又h(3)=1-ln3<0,h(4)=2-ln4>0,
故存在唯一的x0∈(3,4)使得h(x0)=0,即x0-2=lnx0.
当x∈(1,x0)时,h(x)<0,∴g'(x)<0,∴g(x)在(1,x0)上为减函数;
当x∈(x0,+∞)时,h(x)>0,∴g'(x)>0,∴g(x)在(x0,+∞)上为增函数.
∴$g{(x)_{min}}=g({x_0})=\frac{{{x_0}ln{x_0}+2{x_0}-1}}{{{x_0}-1}}=\frac{{{x_0}({x_0}-2)+2{x_0}-1}}{{{x_0}-1}}={x_0}+1$,
∴k<x0+1.
∵x0∈(3,4),
∴x0+1∈(4,5),∵k∈Z,
∴k的最大值为4.
点评 本题主要考查了函数单调性,函数的切线方程求法,以及构造新函数比较大小,属中等难度题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,1] | B. | [$\frac{1}{2}$,1] | C. | [-$\frac{1}{2}$,1] | D. | [0,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
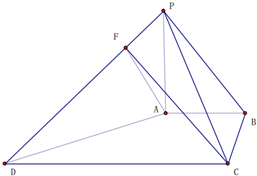 如图,在四棱锥P-ABCD中,已知AB=1,BC=2,CD=4,AB∥CD,BC⊥CD,平面PAB⊥平面ABCD,PA⊥AB,
如图,在四棱锥P-ABCD中,已知AB=1,BC=2,CD=4,AB∥CD,BC⊥CD,平面PAB⊥平面ABCD,PA⊥AB,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 几何题 | 代数题 | 总计 | |
| 男同学 | 22 | 8 | 30 |
| 女同学 | 8 | 12 | 20 |
| 总计 | 30 | 20 | 50 |
| P(k2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com