练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知双曲线E： ﹣ =1（a＞0，b＞0），点F为E的左焦点，点P为E上位于第一象限内的点，P关于原点的对称点为Q，且满足|PF|=3|FQ|，若|OP|=b，则E的离心率为（ ）
    A.
    B.
    C.2
    D.

    【答案】B
    【解析】解：由题意可知：双曲线的右焦点F1 ， 由P关于原点的对称点为Q， 则丨OP丨=丨OQ丨，
    ∴四边形PFQF1为平行四边，
    则丨PF1丨=丨FQ丨，丨PF丨=丨QF1丨，
    由|PF|=3|FQ|，根据椭圆的定义丨PF丨﹣丨PF1丨=2a，
    ∴丨PF1丨=a，|OP|=b，丨OF1丨=c，
    ∴∠OPF1=90°，
    在△QPF1中，丨PQ丨=2b，丨QF1丨=3a，丨PF1丨=a，
    ∴则（2b）2+a2=（3a）2 ， 整理得：b2=2a2 ，
    则双曲线的离心率e= = = ，
    故选B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，圆形纸片的圆心为，半径为1，该纸片上的等边三角形的中心为.、、为圆上的点，，，分别是以，，为底边的等腰三角形.沿虚线剪开后，分别以，，为折痕折起，，，使得、、重合，得到三棱锥.当的边长变化时，所得三棱锥体积的最大值为__________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

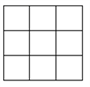
    【题目】在某公司举行的年终庆典活动中，主持人利用随机抽奖软件进行抽奖：由电脑随机生成一张如图所示的33表格，其中1格设奖300元，4格各设奖200元，其余4格各设奖100元，点击某一格即显示相应金额．某人在一张表中随机不重复地点击3格，记中奖的总金额为X元．

    （1）求概率；

    （2）求的概率分布及数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某学校为了了解高中生的艺术素养，从学校随机选取男，女同学各50人进行研究，对这100名学生在音乐、美术、戏剧、舞蹈等多个艺术项目进行多方位的素质测评，并把调查结果转化为个人的素养指标和，制成下图，其中“*”表示男同学，“+”表示女同学.

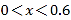
    若，则认定该同学为“初级水平”，若，则认定该同学为“中级水平”，若，则认定该同学为“高级水平”；若，则认定该同学为“具备一定艺术发展潜质”，否则为“不具备明显艺术发展潜质”.

    （I）从50名女同学的中随机选出一名，求该同学为“初级水平”的概率；

    （Ⅱ）从男同学所有“不具备明显艺术发展潜质的中级或高级水平”中任选2名，求选出的2名均为“高级水平”的概率；

    （Ⅲ）试比较这100名同学中，男、女生指标的方差的大小（只需写出结论）.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数 ，的值域是，则实数的取值范围是(　　)

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】商丘市大型购物中心——万达广场将于2018年7月6日全面开业，目前正处于试营业阶段，某按摩椅经销商为调查顾客体验按摩椅的时间，随机调查了50名顾客，体验时间（单位：分钟）落在各个小组的频数分布如下表：

    体验

    时间

    频数

    （1）求这名顾客体验时间的样本平均数，中位数，众数；

    （2）已知体验时间为的顾客中有2名男性，体验时间为的顾客中有3名男性，为进一步了解顾客对按摩椅的评价，现随机从体验时间为和的顾客中各抽一人进行采访，求恰抽到一名男性的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】近年来,郑州经济快速发展,跻身新一线城市行列,备受全国瞩目．无论是市内的井字形快速交通网,还是辐射全国的米字形高铁路网,郑州的交通优势在同级别的城市内无能出其右．为了调查郑州市民对出行的满意程度,研究人员随机抽取了1000名市民进行调查,并将满意程度以分数的形式统计成如下的频率分布直方图,其中．

    （I）求的值；

    （Ⅱ）求被调查的市民的满意程度的平均数,众数,中位数；

    （Ⅲ）若按照分层抽样从,中随机抽取8人,再从这8人中随机抽取2人,求至少有1人的分数在的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，菱形ABCD与正三角形BCE的边长均为2，且平面ABCD⊥平面BCE，FD⊥平面ABCD， ．
    （I）求证：EF∥平面ABCD；
    （II）求证：平面ACF⊥平面BDF．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】不等式组 的解集记为D，命题p：（x，y）∈D，x+2y≥5，命题q：（x，y）∈D，2x﹣y＜2，则下列命题为真命题的是（ ）
    A.p
    B.q
    C.p∨（q）
    D.（p）∨q

    查看答案和解析>>

    同步练习册答案