Question

【题目】如图，菱形ABCD与正三角形BCE的边长均为2，且平面ABCD⊥平面BCE，FD⊥平面ABCD， ．
（I）求证：EF∥平面ABCD；
（II）求证：平面ACF⊥平面BDF．

Answer 1

【答案】证明：（Ⅰ）如图，过点E作EH⊥BC于H，连接HD，∴ ． ∵平面ABCD⊥平面BCE，EH平面BCE，
平面ABCD∩平面BCE=BC，
∴EH⊥平面ABCD，
又∵FD⊥平面ABCD， ，
∴FD∥EH，FD=EH．
∴四边形EHDF为平行四边形．
∴EF∥HD．
∵EF平面ABCD，HD平面ABCD，
∴EF∥平面ABCD． …
（Ⅱ）∵FD⊥面ABCD，∴FD⊥AC，
又四边形ABCD是菱形，∴AC⊥BD，
又FD∩BD=D，∴AC⊥面FBD，
又AC面ACF，从而面ACF⊥面BDF．…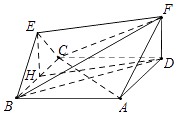

【解析】（Ⅰ）如图，过点E作EH⊥BC于H，连接HD，证明四边形EHDF为平行四边形，根据线面平行的判定定理即可证明EF∥平面ABCD；（Ⅱ）证明AC⊥面FBD，即可证明平面ACF⊥平面BDF．
【考点精析】解答此题的关键在于理解直线与平面平行的判定的相关知识，掌握平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行；简记为：线线平行，则线面平行，以及对平面与平面垂直的判定的理解，了解一个平面过另一个平面的垂线，则这两个平面垂直．