
【题目】已知A(﹣1,0),B(1,0), ![]() =
= ![]() +
+ ![]() ,|
,| ![]() |+|
|+| ![]() |=4
|=4
(1)求P的轨迹E
(2)过轨迹E上任意一点P作圆O:x2+y2=3的切线l1 , l2 , 设直线OP,l1 , l2的斜率分别是k0 , k1 , k2 , 试问在三个斜率都存在且不为0的条件下, ![]() (
( ![]() +
+ ![]() )是否是定值,请说明理由,并加以证明.
)是否是定值,请说明理由,并加以证明.
【答案】
(1)解:如图因为 ![]() =
= ![]() +
+ ![]() ,所以四边形ACPB是平行四边形,
,所以四边形ACPB是平行四边形,
所以| ![]() |=|
|=| ![]() |,
|,
由| ![]() |+|
|+| ![]() |=4,得,|
|=4,得,| ![]() |+|
|+| ![]() |=4,
|=4,
所以P的轨迹是以A,B为焦点的椭圆,a=2,c=1,b= ![]() ,
,
所以方程为 ![]() =1
=1

(2)解:设P(x0,y0),过P的斜率为k的直线为y﹣y0=k(x﹣x0),
由直线与圆O相切可得 ![]() =
= ![]() ,即:
,即: ![]() ,
,
由已知可知k1,k2是方程 ![]() 的两个根,
的两个根,
所以由韦达定理:k1+k2= ![]() ,k1k2=
,k1k2= ![]() ,
,
两式相除: ![]() +
+ ![]() =
= ![]() ,
,
又因为 ![]() =﹣
=﹣ ![]() ,
,
代入上式可得, ![]() (
( ![]() +
+ ![]() )=﹣
)=﹣ ![]() 为一个定值
为一个定值
【解析】(1)利用| ![]() |=|
|=| ![]() |,由|
|,由| ![]() |+|
|+| ![]() |=4,得,|
|=4,得,| ![]() |+|
|+| ![]() |=4,即可求P的轨迹E;(2)所以由韦达定理:k1+k2=
|=4,即可求P的轨迹E;(2)所以由韦达定理:k1+k2= ![]() ,k1k2=
,k1k2= ![]() ,两式相除:
,两式相除: ![]() +
+ ![]() =
= ![]() ,即可得出结论.
,即可得出结论.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知等差数列{an}中,a3=9,a5=17,记数列 ![]() 的前n项和为Sn , 若
的前n项和为Sn , 若 ![]() ,对任意的n∈N*成立,则整数m的最小值为( )
,对任意的n∈N*成立,则整数m的最小值为( )
A.5
B.4
C.3
D.2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为了了解高中生的艺术素养,从学校随机选取男,女同学各50人进行研究,对这100名学生在音乐、美术、戏剧、舞蹈等多个艺术项目进行多方位的素质测评,并把调查结果转化为个人的素养指标![]() 和
和![]() ,制成下图,其中“*”表示男同学,“+”表示女同学.
,制成下图,其中“*”表示男同学,“+”表示女同学.
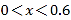
若![]() ,则认定该同学为“初级水平”,若
,则认定该同学为“初级水平”,若![]() ,则认定该同学为“中级水平”,若
,则认定该同学为“中级水平”,若![]() ,则认定该同学为“高级水平”;若
,则认定该同学为“高级水平”;若![]() ,则认定该同学为“具备一定艺术发展潜质”,否则为“不具备明显艺术发展潜质”.
,则认定该同学为“具备一定艺术发展潜质”,否则为“不具备明显艺术发展潜质”.
(I)从50名女同学的中随机选出一名,求该同学为“初级水平”的概率;
(Ⅱ)从男同学所有“不具备明显艺术发展潜质的中级或高级水平”中任选2名,求选出的2名均为“高级水平”的概率;
(Ⅲ)试比较这100名同学中,男、女生指标![]() 的方差的大小(只需写出结论).
的方差的大小(只需写出结论).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】商丘市大型购物中心——万达广场将于2018年7月6日全面开业,目前正处于试营业阶段,某按摩椅经销商为调查顾客体验按摩椅的时间,随机调查了50名顾客,体验时间(单位:分钟)落在各个小组的频数分布如下表:
体验 时间 |
|
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
|
(1)求这![]() 名顾客体验时间的样本平均数
名顾客体验时间的样本平均数![]() ,中位数
,中位数![]() ,众数
,众数![]() ;
;
(2)已知体验时间为![]() 的顾客中有2名男性,体验时间为
的顾客中有2名男性,体验时间为![]() 的顾客中有3名男性,为进一步了解顾客对按摩椅的评价,现随机从体验时间为
的顾客中有3名男性,为进一步了解顾客对按摩椅的评价,现随机从体验时间为![]() 和
和![]() 的顾客中各抽一人进行采访,求恰抽到一名男性的概率.
的顾客中各抽一人进行采访,求恰抽到一名男性的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,郑州经济快速发展,跻身新一线城市行列,备受全国瞩目.无论是市内的井字形快速交通网,还是辐射全国的米字形高铁路网,郑州的交通优势在同级别的城市内无能出其右.为了调查郑州市民对出行的满意程度,研究人员随机抽取了1000名市民进行调查,并将满意程度以分数的形式统计成如下的频率分布直方图,其中![]() .
.

(I)求![]() 的值;
的值;
(Ⅱ)求被调查的市民的满意程度的平均数,众数,中位数;
(Ⅲ)若按照分层抽样从![]() ,
,![]() 中随机抽取8人,再从这8人中随机抽取2人,求至少有1人的分数在
中随机抽取8人,再从这8人中随机抽取2人,求至少有1人的分数在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校高三年级有学生500人,其中男生300人,女生200人,为了研究学生的数学成绩是否与性别有关,现采用分层抽样的方法,从中抽取了100名学生,先统计了他们期中考试的数学分数,然后按性别分为男、女两组,再将两组学生的分数分成5组:[100,110),[110,120),[120,130),[130,140),[140,150]分别加以统计,得到如图所示的频率分布直方图. 
(1)从样本中分数小于110分的学生中随机抽取2人,求两人恰好为一男一女的概率;
(2)若规定分数不小于130分的学生为“数学尖子生”,请你根据已知条件完成2×2列联表,并判断是否有90%的把握认为“数学尖子生与性别有关”?
P(K2≥k0) | 0.100 | 0.050 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 6.635 | 10.828 |
附:K2= ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,菱形ABCD与正三角形BCE的边长均为2,且平面ABCD⊥平面BCE,FD⊥平面ABCD, ![]() .
. 
(I)求证:EF∥平面ABCD;
(II)求证:平面ACF⊥平面BDF.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 的圆心在
的圆心在![]() 轴上,且经过点
轴上,且经过点![]() ,
,![]() .
.
(Ⅰ)求线段AB的垂直平分线方程;
(Ⅱ)求圆![]() 的标准方程;
的标准方程;
(Ⅲ)过点![]() 的直线
的直线![]() 与圆
与圆![]() 相交于
相交于![]() 、
、![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com