
分析 (1)由函数f(x)为奇函数,可得f(-x)+f(x)=0,可得b=d=0.由f(x)=ax3+cx,f′(x)=3ax2+c,在x=-1处取得最大值2,则$\left\{\begin{array}{l}{{f}^{′}(-1)=3a+c=0}\\{-a-c=2}\end{array}\right.$,解得即可得出;
(2)设切点为(x0,y0),则$\left\{\begin{array}{l}{{y}_{0}={x}_{0}^{3}-3{x}_{0}}\\{\frac{{y}_{0}-t}{{x}_{0}-1}=3{x}_{0}^{2}-3}\end{array}\right.$,消去y可得,t=-2${x}_{0}^{3}$+3${x}_{0}^{2}$-3,令u(x)=-2x3+3x2-3,利用导数研究函数u(x)的单调性极值即可得出.
解答 解:(1)∵函数f(x)为奇函数,
∴f(-x)+f(x)=0,2bx2+d=0恒成立,可得b=d=0.
∴f(x)=ax3+cx,f′(x)=3ax2+c,
∵在x=-1处取得最大值2,则$\left\{\begin{array}{l}{{f}^{′}(-1)=3a+c=0}\\{-a-c=2}\end{array}\right.$,
解得a=1,c=-3.
∴f(x)=x3-3x.
(2)设切点为(x0,y0),
则$\left\{\begin{array}{l}{{y}_{0}={x}_{0}^{3}-3{x}_{0}}\\{\frac{{y}_{0}-t}{{x}_{0}-1}=3{x}_{0}^{2}-3}\end{array}\right.$,消去y可得,t=-2${x}_{0}^{3}$+3${x}_{0}^{2}$-3,
令u(x)=-2x3+3x2-3,u′(x)=-6x2+6x=-6x(x-1),
令u′(x)=0,解得x=0,1.
则函数u(x)在(-∞,0),(1,+∞)上单调递减,在(0,1)上单调递增.
u(0)=-3,u(1)=-2.
过点A(1,t)(t≠-2)可作函数f(x)图象的三条切线,
则t的取值范围是(-3,-2).
点评 本题考查了利用导数研究函数的单调性极值、切线方程,考查了推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:解答题
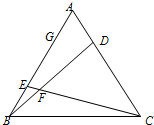 如图,正△ABC中,点D在边AC上,E,G在边AB上,且AB=3AG=6,AD=λAC,AE=(1-λ)AB,(0<λ<1),BD,CE相交于点F
如图,正△ABC中,点D在边AC上,E,G在边AB上,且AB=3AG=6,AD=λAC,AE=(1-λ)AB,(0<λ<1),BD,CE相交于点F查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x1<-2 | B. | x2>0 | C. | x3<1 | D. | x3>2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{8π}{3}$ | B. | $\frac{32π}{3}$ | C. | 8π | D. | $\frac{8\sqrt{2}π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-9,0] | B. | $[0,\frac{5}{3}]$ | C. | $[-9,\frac{5}{3}]$ | D. | $[0,\frac{5}{3})$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com