
(本题满分12分)如图,已知四棱锥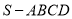 中,
中,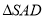 是边长为
是边长为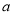 的正三角形,平面
的正三角形,平面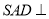 平面
平面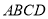 ,四边形
,四边形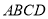 是菱形,
是菱形,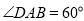 ,
,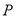 是
是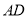 的中点,
的中点,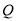 是
是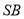 的中点.
的中点.
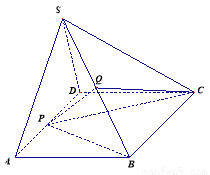
(Ⅰ)求证: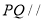 平面
平面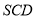 .
.
(Ⅱ)求二面角 的余弦值.
的余弦值.
(Ⅰ)见解析;(Ⅱ)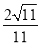 .
.
【解析】
试题分析:(Ⅰ)利用判定定理证明线面平行时,关键是在平面内找一条与已知直线平行的直线,解题时可先直观判断平面内是否已有,若没有,则需作出该直线,常考虑三角形的中位线、平行四边形的对边或过平行线分线段成比例等;要证线线垂直,可通过征到线面垂直得到. (Ⅱ)使用空间向量求解空间角的关键是建立空间直角坐标系后,将空间角转化为向量的运算,然后借助于直线的方向向量和平面的法向量解决立体几何中的计算问题.二面角的范围是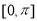 .
.
试题解析:证明(1)取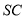 的中点
的中点 ,连接
,连接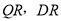 .
.
由题意知 且
且 ,
,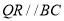 且
且
 ,所以
,所以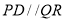 且
且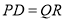 ,即
,即
四边形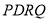 是平行四边形,所以
是平行四边形,所以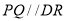 ,
,
又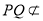 平面
平面 ,
, 平面
平面
所以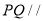 平面
平面 .
.
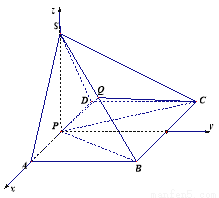
(2)以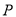 为坐标原点,
为坐标原点,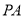 为
为 轴,
轴,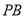 为
为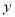 轴,
轴,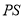 为
为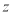 轴,建立如图所示的空间直角坐标系,
轴,建立如图所示的空间直角坐标系, ,则
,则
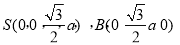
 ,平面
,平面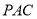 的法向量
的法向量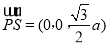 ,设
,设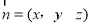 是平面
是平面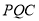 的法向量,
的法向量,
由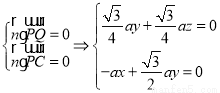 ,令
,令 ,
,
得

又二面角 的平面角是锐角,
的平面角是锐角,
所以二面角 的平面角的余弦值是
的平面角的余弦值是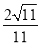
考点:线面平行、二面角


科目:高中数学 来源:2014-2015学年福建省四地六校高三上学期第三次月考理科数学试卷(解析版) 题型:选择题
将函数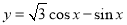 的图像向右平移n个单位后所得图像关于y轴对称,则n的最小正值是( )
的图像向右平移n个单位后所得图像关于y轴对称,则n的最小正值是( )
A.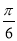 B.
B.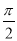 C.
C.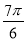 D.
D.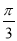
查看答案和解析>>
科目:高中数学 来源:2014-2015学年山西大学附属中学高一上学期期中考试数学试卷(解析版) 题型:选择题
若函数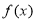 为定义在
为定义在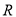 上的奇函数,且在
上的奇函数,且在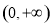 为增函数,又
为增函数,又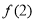
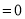 ,则不等式
,则不等式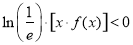 的解集为( )
的解集为( )
A.
B.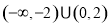
C.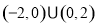
D.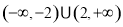
查看答案和解析>>
科目:高中数学 来源:2014-2015学年山西大学附属中学高一上学期期中考试数学试卷(解析版) 题型:选择题
已知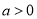 且
且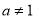 ,下列四组函数中表示相等函数的是( )
,下列四组函数中表示相等函数的是( )
A.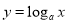 与
与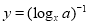
B.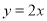 与
与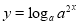
C.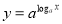 与
与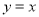
D.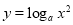 与
与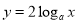
查看答案和解析>>
科目:高中数学 来源:2014-2015学年黑龙江省绥化市三校高二上学期期中联考数学试卷(解析版) 题型:填空题
设圆过双曲线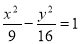 的一个顶点和一个焦点,圆心在此双曲线上,则圆心到双曲线中心的距离为 .
的一个顶点和一个焦点,圆心在此双曲线上,则圆心到双曲线中心的距离为 .
查看答案和解析>>
科目:高中数学 来源:2014-2015学年黑龙江省绥化市三校高二上学期期中联考数学试卷(解析版) 题型:选择题
已知动点 满足
满足 ,则点P的轨迹是 ( )
,则点P的轨迹是 ( )
A.两条相交直线 B.抛物线 C.双曲线 D.椭圆
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com