
分析 (Ⅰ)利用三角函数恒等变换的应用化简函数解析式可得f(x)=sin(x-$\frac{π}{6}$),代入x=$\frac{π}{3}$,即可计算求值.
(Ⅱ)由-$\frac{π}{6}$≤x≤$\frac{5π}{6}$,可求-$\frac{π}{3}$≤x-$\frac{π}{6}$≤$\frac{2π}{3}$,利用正弦函数的性质即可得解f(x)在区间$[-\frac{π}{6},\frac{5π}{6}]$上的最大值和最小值.
解答 (本小题满分13分)
解:(Ⅰ)∵由已知$f(x)=\;{sin^2}\frac{x}{2}+\frac{{\sqrt{3}}}{2}sinx-\frac{1}{2}$=$\frac{1-cosx}{2}$+$\frac{\sqrt{3}}{2}$sinx-$\frac{1}{2}$,…(3分)
=$\frac{\sqrt{3}}{2}$sinx-$\frac{1}{2}$cosx=sin(x-$\frac{π}{6}$),…(4分)
∴f($\frac{π}{3}$)=sin($\frac{π}{3}$-$\frac{π}{6}$)=$\frac{1}{2}$…(6分)
(Ⅱ)∵-$\frac{π}{6}$≤x≤$\frac{5π}{6}$,∴-$\frac{π}{3}$≤x-$\frac{π}{6}$≤$\frac{2π}{3}$,…(9分)
当x-$\frac{π}{6}$=-$\frac{π}{3}$,即x=-$\frac{π}{6}$时,fmin(x)=-$\frac{\sqrt{3}}{2}$,…(11分)
当x-$\frac{π}{6}$=$\frac{π}{2}$,即x=$\frac{2π}{3}$时,fmax(x)=1…(13分)
点评 本题主要考查了三角函数恒等变换的应用,三角函数化简求值,考查了正弦函数的图象和性质的应用,属于基础题.


科目:高中数学 来源: 题型:填空题
 如图,已知PA⊥平面ABC,AC⊥AB,AP=BC,∠CBA=30°,D、E分别是BC、AP的中点.则异面直线AC与DE所成角的正切值为$\sqrt{7}$.
如图,已知PA⊥平面ABC,AC⊥AB,AP=BC,∠CBA=30°,D、E分别是BC、AP的中点.则异面直线AC与DE所成角的正切值为$\sqrt{7}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1)∪(2,+∞) | B. | [1,2] | C. | [-1,1)∪(2,3] | D. | [-1,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 男 | 女 | 总计 | |
| 爱好 | 40 | 20 | 60 |
| 不爱好 | 20 | 30 | 50 |
| 总计 | 60 | 50 | 110 |
| P(K2≥K0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| K0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| A. | 有99%以上的把握认为“爱好体育运动与性别有关” | |
| B. | 有99%以上的把握认为“爱好体育运动与性别无关” | |
| C. | 在犯错误的概率不超过0.1%的前提下,认为“爱好体育运动与性别有关” | |
| D. | 在犯错误的概率不超过0.1%的前提下,认为“爱好体育运动与性别无关” |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a+c≤0 | B. | a+c>0 | C. | a+c≤0 | D. | a+c<0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
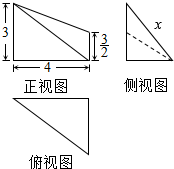 某几何体的三视图如图所示,若该几何体的体积为3$\sqrt{7}$,则侧视图中线段的长度x的值是( )
某几何体的三视图如图所示,若该几何体的体积为3$\sqrt{7}$,则侧视图中线段的长度x的值是( )| A. | 5 | B. | 4 | C. | 2$\sqrt{7}$ | D. | $\sqrt{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
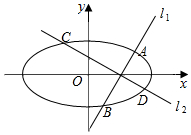 在平面直角坐标系中,已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,F为椭圆的右焦点,过点F任作一条直线l1,交椭圆E于A,B两点,当l1垂直于x轴时,|AB|=1.
在平面直角坐标系中,已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,F为椭圆的右焦点,过点F任作一条直线l1,交椭圆E于A,B两点,当l1垂直于x轴时,|AB|=1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com