
 如图所示,AB是圆O的直径,延长BA至C,使AC=$\frac{1}{3}$BC,过C作圆O的切割线交圆O于M、N两点,且AM=MN.
如图所示,AB是圆O的直径,延长BA至C,使AC=$\frac{1}{3}$BC,过C作圆O的切割线交圆O于M、N两点,且AM=MN.分析 (1)连接AN,说明AN⊥BN,BN∥OM,然后证明∠AOM=∠ABN.
(2)根据切割线定理得,CM×CN=CA×CB=3OA2,求出BN,在Rt△ABN中,求解AN即可.
解答 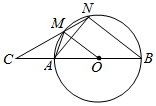 解:(1)连接AN,∵AB是圆O的直径,∴AN⊥BN,
解:(1)连接AN,∵AB是圆O的直径,∴AN⊥BN,
∵AM=MN,∴OM⊥AN,∴BN∥OM,
∴∠AOM=∠ABN.
(2)∵$AC=\frac{1}{3}BC$,∴AC=AO,
∵OM∥BN,∴$\frac{CM}{MN}=\frac{CO}{BO}=2$,∴MN=2,∴CM=4,∴CN=6,
根据切割线定理得,CM×CN=CA×CB=3OA2,∴$OA=2\sqrt{2}$,又$\frac{OM}{BN}=\frac{2}{3}$,
∴$BN=3\sqrt{2}$,
在Rt△ABN中,AN2=AB2-BN2=32-18=14,
∴$AN=\sqrt{14}$.
点评 本题考查与圆有关的线段成比例问题,切割线定理的应用,考查分析问题解决问题的能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 班级 | 优秀 | 非优秀 | 合计 |
| 甲班 | 18 | ||
| 乙班 | 43 | ||
| 合计 | 110 |
| P(K2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 |
| k0 | 1.323 | 2.072 | 2.706 | 3.841 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 2$\sqrt{2}$ | C. | 4 | D. | 2$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\sqrt{5}$ | C. | 3 | D. | 2$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 10 | C. | 12 | D. | 16 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com