
| A. | [$\frac{1}{2}$,17] | B. | [1,17] | C. | [1,$\sqrt{17}$] | D. | [$\frac{\sqrt{2}}{2}$,$\sqrt{17}$] |
分析 由题意作平面区域,而x2+(y+2)2的几何意义是点A(0,-2)与阴影内的点的距离的平方,从而结合图象解得.
解答 解:由题意作平面区域如下, ,
,
x2+(y+2)2的几何意义是点A(0,-2)与阴影内的点的距离的平方,
而点A到直线y=x-1的距离d=$\frac{|1-0-2|}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$,
B(-1,2),故|AB|=$\sqrt{(-1)^{2}+{4}^{2}}$=$\sqrt{17}$,
故($\frac{\sqrt{2}}{2}$)2≤x2+(y+2)2≤($\sqrt{17}$)2,
即$\frac{1}{2}$≤x2+(y+2)2≤17,
故选:A.
点评 本题考查了线性规划的变形应用及数形结合的思想应用,同时考查了转化思想的应用.


科目:高中数学 来源: 题型:选择题
 某科技研究所对一批新研发的产品长度进行检测(单位:mm),如图是检测结果的频率分布直方图,据此估计这批产品的中位数为( )
某科技研究所对一批新研发的产品长度进行检测(单位:mm),如图是检测结果的频率分布直方图,据此估计这批产品的中位数为( )| A. | 20 | B. | 22.5 | C. | 22.75 | D. | 25 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
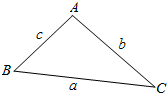 (1)如图所示.在△ABC中,射影定理可表示为a=b•cosC+c•cosB.其中a,b,c分别为角A,B,C的对边,类比上述定理.写出对空间四面体性质的猜想.
(1)如图所示.在△ABC中,射影定理可表示为a=b•cosC+c•cosB.其中a,b,c分别为角A,B,C的对边,类比上述定理.写出对空间四面体性质的猜想.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ${∫}_{0}^{π}$cosxdx | B. | ${∫}_{0}^{\frac{π}{2}}$cosxdx+|${∫}_{\frac{π}{2}}^{π}$cosxdx| | ||
| C. | ${∫}_{0}^{π}$2sinxdx | D. | ${∫}_{0}^{π}$2|cosx|dx |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com