
分析 (1)当x1=0,x2=1,x3=2时,化简f(x)=x(x-1)(x-2),再求导并令f′(x)=3x2-6x+2<0,从而解得;
(2)先求导f′(x)=(x-x2)(x-x3)+(x-x1)(x-x3)+(x-x1)(x-x2),从而可判断f′(x1)=(x1-x2)(x1-x3)>0,f′(x2)<0,f′(x3)>0,从而由函数零点的判定定理证明即可;
(3)易知f′(α)=f′(β)=0,再求得f′($\frac{{x}_{1}+x{\;}_{2}}{2}$)=($\frac{{x}_{1}+x{\;}_{2}}{2}$-x2)($\frac{{x}_{1}+x{\;}_{2}}{2}$-x3)+($\frac{{x}_{1}+x{\;}_{2}}{2}$-x1)($\frac{{x}_{1}+x{\;}_{2}}{2}$-x3)+($\frac{{x}_{1}+x{\;}_{2}}{2}$-x1)($\frac{{x}_{1}+x{\;}_{2}}{2}$-x2)=-$\frac{1}{4}$(x1-x2)2<0,f′($\frac{x{\;}_{2}+x{\;}_{3}}{2}$)<0,从而结合二次函数的图象可比较四个数的大小.
解答 解:(1)当x1=0,x2=1,x3=2时,
f(x)=x(x-1)(x-2),
令f′(x)=3x2-6x+2<0解得,
$\frac{3-\sqrt{3}}{3}$<x<$\frac{3+\sqrt{3}}{3}$,
故函数f(x)的减区间为($\frac{3-\sqrt{3}}{3}$,$\frac{3+\sqrt{3}}{3}$);
(2)证明:∵f(x)=(x-x1)(x-x2)(x-x3),
∴f′(x)=(x-x2)(x-x3)+(x-x1)(x-x3)+(x-x1)(x-x2),
又∵x1<x2<x3,
∴f′(x1)=(x1-x2)(x1-x3)>0,
f′(x2)=(x2-x1)(x2-x3)<0,
f′(x3)=(x3-x2)(x3-x1)>0,
故函数f′(x)在(x1,x2),(x2,x3)上分别有一个零点,
故方程f′(x)=0有两个不相等的实数根;
(3)∵方程f′(x)=0的两个实数根是α,β(α<β),
∴f′(α)=f′(β)=0,
而f′($\frac{{x}_{1}+x{\;}_{2}}{2}$)=($\frac{{x}_{1}+x{\;}_{2}}{2}$-x2)($\frac{{x}_{1}+x{\;}_{2}}{2}$-x3)+($\frac{{x}_{1}+x{\;}_{2}}{2}$-x1)($\frac{{x}_{1}+x{\;}_{2}}{2}$-x3)+($\frac{{x}_{1}+x{\;}_{2}}{2}$-x1)($\frac{{x}_{1}+x{\;}_{2}}{2}$-x2)
=-$\frac{1}{4}$(x1-x2)2<0,
f′($\frac{x{\;}_{2}+x{\;}_{3}}{2}$)=($\frac{x{\;}_{2}+x{\;}_{3}}{2}$-x2)($\frac{x{\;}_{2}+x{\;}_{3}}{2}$-x3)+($\frac{x{\;}_{2}+x{\;}_{3}}{2}$-x1)($\frac{x{\;}_{2}+x{\;}_{3}}{2}$-x3)+($\frac{x{\;}_{2}+x{\;}_{3}}{2}$-x1)($\frac{x{\;}_{2}+x{\;}_{3}}{2}$-x2)
=-$\frac{1}{4}$(x3-x2)2<0,
再结合二次函数的图象可知,
α<$\frac{{x}_{1}+x{\;}_{2}}{2}$<$\frac{x{\;}_{2}+x{\;}_{3}}{2}$<β.
点评 本题考查了导数的综合应用及二次函数的性质,同时考查了函数的零点的判定定理的应用,属于中档题.


科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,侧面PCD⊥底面ABCD(1)若M,N分别为PC,BD的中点,求证:MN∥平面PAD;
如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,侧面PCD⊥底面ABCD(1)若M,N分别为PC,BD的中点,求证:MN∥平面PAD;查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某市为了节约能源,拟出台“阶梯电价”制度,即制定住户月用电量的临界值a,若某住户某月用电量不超过a度,则按平价计费;若某月用电量超过a度,则超出部分按议价计费.未超出分布按平价计费.为确定a的值,随机调查了该市100户的月用电量,工作人员已将90户的用电量填在了下面的频率分布表中,最后10户的月用电量(单位:度)为:18 63 43 119 65 77 29 97 52 100
某市为了节约能源,拟出台“阶梯电价”制度,即制定住户月用电量的临界值a,若某住户某月用电量不超过a度,则按平价计费;若某月用电量超过a度,则超出部分按议价计费.未超出分布按平价计费.为确定a的值,随机调查了该市100户的月用电量,工作人员已将90户的用电量填在了下面的频率分布表中,最后10户的月用电量(单位:度)为:18 63 43 119 65 77 29 97 52 100| 组别 | 月用电量 | 频数统计 | 频数 | 频率 |
| 1 | [0,20) |  | ||
| 2 | [20,40) | 正正一 | ||
| 3 | [40,60) | 正正正正 | ||
| 4 | [60,80) | 正正正正正 | ||
| 5 | [80,100) | 正正正正 | ||
| 6 | [100,120) |  |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
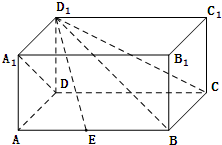 在四棱柱ABCD-A1B1C1D1中,侧棱DD1⊥底面ABCD,底面ABCD是矩形,且AD=AA1.
在四棱柱ABCD-A1B1C1D1中,侧棱DD1⊥底面ABCD,底面ABCD是矩形,且AD=AA1.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,在△ABC中,CD是∠ACB的角平分线,△ADC的外接圆交BC于点E,AB=2AC=6,EC=6,则AD的长为$\frac{3}{2}$.
如图,在△ABC中,CD是∠ACB的角平分线,△ADC的外接圆交BC于点E,AB=2AC=6,EC=6,则AD的长为$\frac{3}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com