
分析 (1)由?x∈R,$\frac{1}{m}$-4≥f(x)恒成立,可得m+$\frac{1}{m}$≥x-|x+2|-|x-3|+4,求出右边的最大值,即可求m的取值范围;
(2)利用对数的性质及基本不等式,即可证明结论.
解答 (1)解:∵?x∈R,$\frac{1}{m}$-4≥f(x)恒成立,
∴m+$\frac{1}{m}$≥x-|x+2|-|x-3|+4,
令g(x)=x-|x+2|-|x-3|+4,则g(x)在(-∞,3)上是增函数,
(3,+∞)上是减函数,g(x)max=g(3)=2,
∴m+$\frac{1}{m}$≥2,∴m>0;
(2)证明:m>0,可得m+3>m+2>m+1>1,
则lg(m+3)>lg(m+2)>lg(m+1)>lg1=0,
∵lg(m+1)lg(m+3)<$[\frac{lg(m+1)+lg(m+3)}{2}]^{2}$=$\frac{[lg(m+1)(m+3)]^{2}}{4}$<lg2(m+2),
∴$\frac{lg(m+2)}{lg(m+1)}>\frac{lg(m+3)}{lg(m+2)}$,
∴log(m+1)(m+2)>log(m+2)(m+3).
点评 本题考查恒成立问题,考查函数的最值,考查对数的性质、基本不等式的运用,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | c<b<a | B. | c<a<b | C. | b<a<c | D. | a<c<b |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 28 | B. | 26 | C. | 24 | D. | 22 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
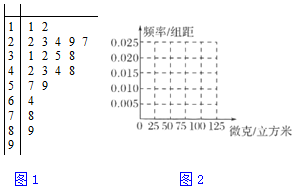
| 组别 | PM2.5浓度(微粒、立方米) | 频数(天) | 频率 |
| 第一组 | (0,25] | 5 | 0.25 |
| 第二组 | (25,50] | 10 | 0.5 |
| 第三组 | (50,75] | 3 | 0.15 |
| 第四组 | (75,100] | 2 | 0.1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com