
分析 通过两角差的正切公式变形可知an=$\frac{tann-tan(n-1)}{tan1}$-1,进而利用分组法求和即可.
解答 证明:∵tan(A-B)=$\frac{tanA-tanB}{1+tanA•tanB}$,
∴tanA•tanB=$\frac{tanA-tanB}{tan(A-B)}$-1,
又∵数列{an}的通项公式an=tann•tan(n-1),
∴an=$\frac{tann-tan(n-1)}{tan[n-(n-1)]}$-1=$\frac{tann-tan(n-1)}{tan1}$-1,
∴Sn=$\frac{1}{tan1}$[tan1-tan0+tan2-tan1+tan3-tan2+…+tann-tan(n-1)]-n
=$\frac{1}{tan1}$(tann-tan0)-n
=$\frac{1}{tan1}$•tann-n,
令A=$\frac{1}{tan1}$,B=-1,则对于任意n∈N+存在常数A、B使得Sn=Atann+Bn.
点评 本题考查数列的求和,涉及两角差的正切公式,考查并项相消法求数列的和,注意解题方法的积累,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | M∪N=M | B. | (∁RM)∩N=R | C. | (∁RM)∩N=∅ | D. | M∩N=M |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
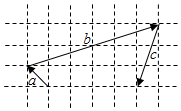
| A. | -8 | B. | -4 | C. | 4 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 24 | B. | 18 | C. | 16 | D. | 10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com