Question

2．为了解甲、乙两校高三学生某次数学联赛成绩情况，从这两学校中分别随机抽取30名学生成绩（百分制）作为样本，样本数据如下：
甲校：41 45 54 56 60 63 63 65 64 66 62 67 70 70 72
     72 74 74 81 83 85 85 87 86 86 89 91 92 98 99
乙校：46 55 62 64 70 73 72 72 73 75 77 77 79 79 79
     82 83 81 84 85 84 88 87 89 88 84 91 94 96 98
（1）若甲校所有参赛学生中每名学生被抽取的概率为0.15，求甲校高三年级参赛学生总人数；
（2）根据两组数据完成两校学生成绩的茎叶图；并通过茎叶图比较两校学生成绩的平均分及分散程度（不要求计算出具体值，给出结论即可）；
（3）从样本中甲乙两校高三年级参赛学生成绩不及格（低于60分为不及格）的学生中随机抽取2人，求至少抽到一名乙校学生的概率．

Answer 1

分析 （1）根据频率与频数、样本容量的关系，即可求出参数学生总人数；
（2）画出学生成绩的茎叶图，由茎叶图得出乙校学生的成绩平均分较高，成绩较集中；
（3）用列举法求出从甲乙两校不及格的同学中随机抽取两人的基本事件数，以及对应的事件数，计算所求的概率．

解答 解：（1）甲校高三年级参数学生总人数为M=$\frac{30}{0.15}$=200；
（2）两校学生成绩的茎叶图如右：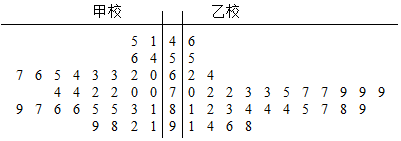

由茎叶图可知乙校学生的成绩平均分要高，且成绩比较集中，
甲校学生的成绩平均分要低，且成绩比较分散；
（3）由茎叶图可知，甲校有4位同学成绩不及格，分别记为：1、2、3、4，
乙校有2位同学成绩不及格，分别记为5、6，则从两校不及格的同学中随机抽取两人，有如下可能：
（1、2），（1、3），（1、4），（1、5），（1、6），（2、3），（2、4），（2、5），（2、6），
（3、4），（3、5），（3、6），（4、5），（4、6），（5、6）共有15个基本事件；
其中，乙校包含至少有一名学生成绩不及格的事件为A，则A包含9个基本事件，如下；
（1、5），（1、6），（2、5），（2、6），（3、5），（3、6），（4、5），（4、6），（5、6）；
所求的概率为P=$\frac{9}{15}$=$\frac{3}{5}$．

点评 本题考查了茎叶图的应用问题，也考查了用列举法求古典概型的概率问题，是基础题目．