
 (米)是时间
(米)是时间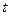 (0≤
(0≤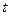 ≤24,单位:小时)的函数,下面是不同时间的水深数据:
≤24,单位:小时)的函数,下面是不同时间的水深数据:
 的图像.
的图像.
 的表达式;
的表达式; ⑵船舶要在一天之内在港口停留时间最长,就应从凌晨1点(1点到5点都可以)进港,而下午的17点(即13点到17点之间)前离港,在港内停留的时间最长为16小时
⑵船舶要在一天之内在港口停留时间最长,就应从凌晨1点(1点到5点都可以)进港,而下午的17点(即13点到17点之间)前离港,在港内停留的时间最长为16小时 在一个周期内由最大变到最小需9-3=6小时,此为半个周期,所以函数的最小正周期为12小时,因此
在一个周期内由最大变到最小需9-3=6小时,此为半个周期,所以函数的最小正周期为12小时,因此 .
. 时,
时, ;
; 时,
时, ;故
;故
 .
. 应大于等于7+4.5=11.5(米).
应大于等于7+4.5=11.5(米).

 =0,则1≤
=0,则1≤ ≤5;取
≤5;取 =1,则13≤
=1,则13≤ ≤17;而取
≤17;而取 =2时,则25≤
=2时,则25≤ ≤29(不合题意).
≤29(不合题意).

 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 (米)是时间
(米)是时间 (
( ,单位:时)的函数,记作
,单位:时)的函数,记作 , 下面是某日水深的数据:
, 下面是某日水深的数据:| t/h | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| y/m | 10.0 | 13.0 | 9.9 | 7.0 | 10.0 | 13.0 | 10.1 | 7.0 | 10.0 |
 的曲线可以近似的看成函数
的曲线可以近似的看成函数 的图象,根据以上的数据,可得函数
的图象,根据以上的数据,可得函数 的近似表达式为 .
的近似表达式为 . 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com