
已知函数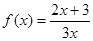 , 数列
, 数列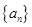 满足
满足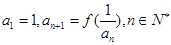 .
.
(1)求数列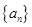 的通项公式;
的通项公式;
(2)令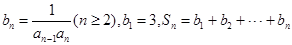 ,若
,若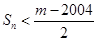 对一切
对一切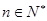 成立,求最小正整数m.
成立,求最小正整数m.
 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案科目:高中数学 来源: 题型:解答题
已知函数f(x)= ,数列{an}满足:2an+1-2an+an+1an=0且an≠0.数列{bn}中,b1=f(0)且bn=f(an-1).
,数列{an}满足:2an+1-2an+an+1an=0且an≠0.数列{bn}中,b1=f(0)且bn=f(an-1).
(1)求证:数列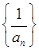 是等差数列;
是等差数列;
(2)求数列{|bn|}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(2013·安徽高考)设数列{an}满足a1=2,a2+a4=8,且对任意n∈N*,函数f(x)=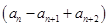 x+an+1cos x-an+2sin x满足f′
x+an+1cos x-an+2sin x满足f′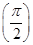 =0.
=0.
(1)求数列{an}的通项公式;
(2)若bn=2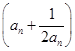 ,求数列{bn}的前n项和Sn.
,求数列{bn}的前n项和Sn.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
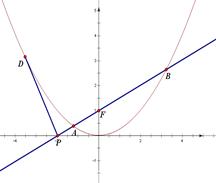
抛物线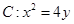 ,直线
,直线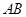 过抛物线
过抛物线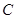 的焦点
的焦点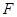 ,交
,交 轴于点
轴于点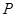 .
.
(1)求证: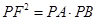 ;
;
(2)过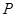 作抛物线
作抛物线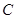 的切线,切点为
的切线,切点为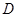 (异于原点),
(异于原点),
(ⅰ)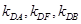 是否恒成等差数列,请说明理由;
是否恒成等差数列,请说明理由;
(ⅱ)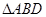 重心的轨迹是什么图形,请说明理由.
重心的轨迹是什么图形,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知数列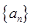 ,
,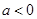 满足
满足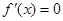 ,
,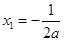 ,
,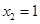 ,
,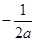 .
.
(1)求证:数列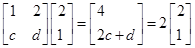 是等差数列,并求数列
是等差数列,并求数列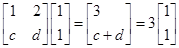 的通项公式;
的通项公式;
(2)设数列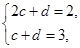 满足
满足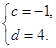 ,对于任意给定的正整数
,对于任意给定的正整数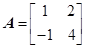 ,是否存在正整数
,是否存在正整数 ,
, (
(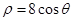 ),使得
),使得 ,
,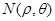 ,
,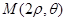 成等差数列?若存在,试用
成等差数列?若存在,试用 表示
表示 ,
,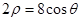 ;若不存在,说明理由.
;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
一个三角形数表按如下方式构成(如图:其中项数 ):第一行是以4为首项,4为公差的等差数列,从第二行起,每一个数是其肩上两个数的和,例如:
):第一行是以4为首项,4为公差的等差数列,从第二行起,每一个数是其肩上两个数的和,例如: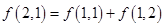 ;
;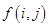 为数表中第
为数表中第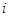 行的第
行的第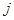 个数.
个数.
求第2行和第3行的通项公式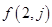 和
和 ;
;
证明:数表中除最后2行外每一行的数都依次成等差数列,并求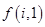 关于
关于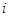 (
(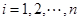 )的表达式;
)的表达式;
(3)若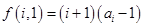 ,
,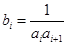 ,试求一个等比数列
,试求一个等比数列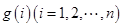 ,使得
,使得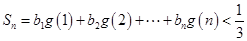 ,且对于任意的
,且对于任意的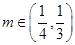 ,均存在实数
,均存在实数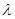 ?,当
?,当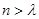 时,都有
时,都有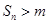 .
.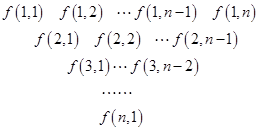
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知数列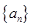 中,
中,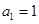 ,对任意的
,对任意的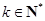 ,
,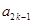 、
、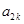 、
、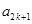 成等比数列,公比为
成等比数列,公比为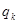 ;
;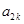 、
、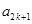 、
、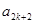 成等差数列,公差为
成等差数列,公差为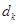 ,且
,且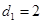 .
.
(1)写出数列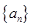 的前四项;
的前四项;
(2)设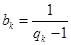 ,求数列
,求数列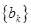 的通项公式;
的通项公式;
(3)求数列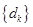 的前
的前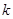 项和
项和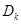 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com