
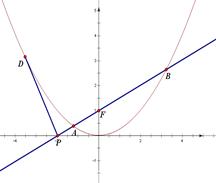
抛物线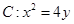 ,直线
,直线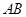 过抛物线
过抛物线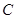 的焦点
的焦点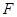 ,交
,交 轴于点
轴于点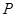 .
.
(1)求证: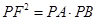 ;
;
(2)过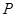 作抛物线
作抛物线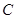 的切线,切点为
的切线,切点为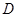 (异于原点),
(异于原点),
(ⅰ)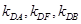 是否恒成等差数列,请说明理由;
是否恒成等差数列,请说明理由;
(ⅱ)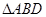 重心的轨迹是什么图形,请说明理由.
重心的轨迹是什么图形,请说明理由.
(1) 即证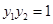 (2) 能 抛物线
(2) 能 抛物线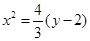
解析试题分析:(1)由于点F的坐标已知,所以可假设直线AB的方程(依题意可得直线AB的斜率存在).写出点P的坐标,联立直线方程与抛物线方程消去y,即可得到一个关于x的一元二次方程,写出韦达定理,再根据欲证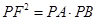 转化为点的坐标关系.
转化为点的坐标关系.
(2)(ⅰ)根据提议分别写出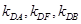 ,结合韦达定理验证
,结合韦达定理验证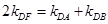 是否成立.
是否成立.
(ⅱ)由三角形重心的坐标公式,结合韦达定理,消去参数k即可得到重心的轨迹.
(1)因为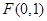 ,所以假设直线AB为
,所以假设直线AB为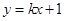 ,
,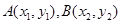 ,所以点
,所以点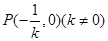 .联立
.联立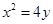 可得,
可得,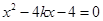 ,所以
,所以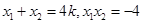 .因为
.因为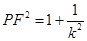 ,
,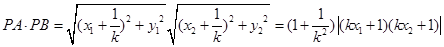
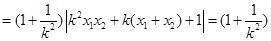 .所以
.所以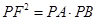 .
.
(2)(ⅰ)设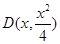 ,
,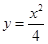 的导数为
的导数为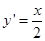 .所以可得
.所以可得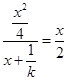 ,即可得
,即可得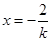 .即得
.即得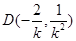 .
.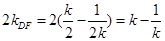 .
.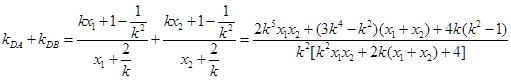
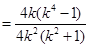
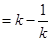 .所以可得
.所以可得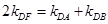 即
即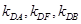 是否恒成等差数列.
是否恒成等差数列.
(ⅱ)因为 重心的坐标为
重心的坐标为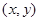 由题意可得
由题意可得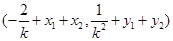 .即
.即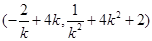 ,
,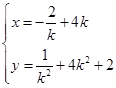 消去k可得
消去k可得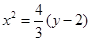 .
.
考点:1.抛物线的性质.2.解方程的思想.3.等差数列的证明.4.三角形的重心的公式.5.运算能力.6.分析问题和解决问题的能力、以及等价转化的数学思想.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
已知{an}是正数组成的数列,a1=1,且点(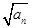 ,an+1)( n ∈N*)在函数y=x2+1的图象上.
,an+1)( n ∈N*)在函数y=x2+1的图象上.
(1)求数列{an}的通项公式;
(2)若数列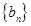 满足b1=1,
满足b1=1,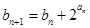 ,求证:
,求证: .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知集合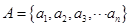 ,
,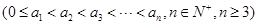
具有性质 :对任意的
:对任意的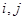
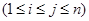 ,
,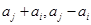 至少有一个属于
至少有一个属于 .
.
(1)分别判断集合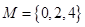 与
与 是否具有性质
是否具有性质 ;
;
(2)求证:①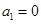 ;
;
②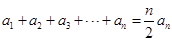 ;
;
(3)当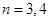 或
或 时集合
时集合 中的数列
中的数列 是否一定成等差数列?说明理由.
是否一定成等差数列?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com