
分析 设围成的矩形场地的长为am,宽为bm,由题意可得a+2b=40,则矩形的面积S=ab,由基本不等式即可得到所求最大值.
解答 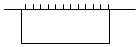 解:设围成的矩形场地的长为am,宽为bm,
解:设围成的矩形场地的长为am,宽为bm,
由题意可得a+2b=40,
则围成的场地面积设为S,
即有S=ab=$\frac{1}{2}$a•2b≤$\frac{1}{2}$($\frac{a+2b}{2}$)2
=$\frac{1}{2}$•($\frac{40}{2}$)2=200.
当且仅当a=2b,即a=20m,b=10m时,取得最大值200m2.
则围成的场地面积最大为200m2.
点评 本题考查数学模型的应用题的解法,注意运用根据题意,列出关系式,运用基本不等式求得最值,考查运算能力,属于基础题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
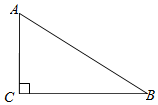 如图,在Rt△ABC中,∠ACB=90°,|BC|=4,|AC|=3,一曲线E过点A,动点P在曲线E运动,且保持|PC|+|PB|的值不变.
如图,在Rt△ABC中,∠ACB=90°,|BC|=4,|AC|=3,一曲线E过点A,动点P在曲线E运动,且保持|PC|+|PB|的值不变.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com