
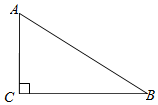
 如图,在Rt△ABC中,∠ACB=90°,|BC|=4,|AC|=3,一曲线E过点A,动点P在曲线E运动,且保持|PC|+|PB|的值不变.
如图,在Rt△ABC中,∠ACB=90°,|BC|=4,|AC|=3,一曲线E过点A,动点P在曲线E运动,且保持|PC|+|PB|的值不变.分析 (I)由椭圆定义可知E为以B,C为焦点的椭圆,利用待定系数法求出椭圆方程;
(II)求出Q的坐标,设M,N坐标,利用重心坐标公式得出M,N坐标的关系求出MN中点,代入椭圆方程化简得出直线l的斜率,从而得出直线l的方程.
解答 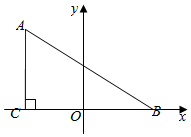 解:(I)以CB所在直线为x轴,CB中垂线为y轴建立直角坐标系,
解:(I)以CB所在直线为x轴,CB中垂线为y轴建立直角坐标系,
∵∠ACB=90°,|BC|=4,|AC|=3,∴AB=5.
设P(x,y).则|PC|+|PB|=|AC|+|AB|=8.
∴动点P的轨迹是以B,C为焦点的椭圆,
设椭圆方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$,
则c=|OB|=2,a=$\frac{|PA|+|PB|}{2}$=4,∴b2=a2-c2=12.
∴曲线E的方程为$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{12}$=1.
(II)B(2,0),Q(0,2$\sqrt{3}$),设M(x1,y1),N(x2,y2),
∵△QMN的重心为B点.
∴$\left\{\begin{array}{l}{\frac{{x}_{1}+{x}_{2}+0}{3}=2}\\{\frac{{y}_{1}+{y}_{2}+2\sqrt{3}}{3}=0}\end{array}\right.$,则$\left\{\begin{array}{l}{{x}_{1}+{x}_{2}=6}\\{{y}_{1}+{y}_{2}=-2\sqrt{3}}\end{array}\right.$,
∴MN的中点为(3,-$\sqrt{3}$).
∵$\left\{\begin{array}{l}{\frac{{{x}_{1}}^{2}}{16}+\frac{{{y}_{1}}^{2}}{12}=1}\\{\frac{{{x}_{2}}^{2}}{16}+\frac{{{y}_{2}}^{2}}{12}=1}\end{array}\right.$,两式相减的得:$\frac{({x}_{1}+{x}_{2})({x}_{1}-{x}_{2})}{16}+\frac{({y}_{1}+{y}_{2})({y}_{1}-{y}_{2})}{12}=0$,
即$\frac{3({x}_{1}-{x}_{2})}{8}-\frac{\sqrt{3}({y}_{1}-{y}_{2})}{6}=0$,∴$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$=$\frac{3\sqrt{3}}{4}$.即直线l的斜率为$\frac{3\sqrt{3}}{4}$.
∴直线l方程为y+$\sqrt{3}$=$\frac{3\sqrt{3}}{4}$(x-3),即3$\sqrt{3}$x-4y-13$\sqrt{3}$=0.
点评 本题考查了椭圆的定义,直线与椭圆的关系,属于中档题.


 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{32π}{3}$ | B. | $\frac{16π}{3}$ | C. | 4$\sqrt{3}$π | D. | 16π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
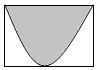 如图,长方形的面积为2,将100颗豆子随机地撒在长方形内,其中恰好有60 颗豆子落在阴影部分内,则用随机模拟的方法可以估计图中阴影部分的面积为$\frac{6}{5}$.
如图,长方形的面积为2,将100颗豆子随机地撒在长方形内,其中恰好有60 颗豆子落在阴影部分内,则用随机模拟的方法可以估计图中阴影部分的面积为$\frac{6}{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 60° | B. | 60°或120° | C. | 30°或150° | D. | 120° |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com