
分析 本题是一个计数原理的应用,当甲车排第①个时,乙车可排2、3、4号;当甲车排第②个时,乙车可排3、4号;当甲车排第③个时,乙车只可排4号;除甲、乙两车外,在其余5辆车中任意选取2辆按顺序排列,根据加法和乘法原理得到结果.
解答 解:由题意知,本题是一个计数原理的应用,
当甲车排第①个时,乙车可排2、3、4号,有3种选择;
当甲车排第②个时,乙车可排3、4号,有2种选择;
当甲车排第③个时,乙车只可排4号,只有1种选择;
除甲、乙两车外,在其余5辆车中任意选取2辆按顺序排列,有A52种选法;
因此共有:(3+2+1)A52=120种不同的调度方案.
故答案为:120
点评 本题考查分类计数和分步计数,是一个计数原理的综合应用,对于复杂一点的计数问题,有时分类以后,每类方法并不都是一步完成的,必须在分类后又分步.


科目:高中数学 来源: 题型:选择题
| A. | (2,1) | B. | (4,7) | C. | (-2,-1) | D. | (-4,-7) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
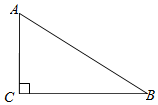 如图,在Rt△ABC中,∠ACB=90°,|BC|=4,|AC|=3,一曲线E过点A,动点P在曲线E运动,且保持|PC|+|PB|的值不变.
如图,在Rt△ABC中,∠ACB=90°,|BC|=4,|AC|=3,一曲线E过点A,动点P在曲线E运动,且保持|PC|+|PB|的值不变.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 22016 | B. | 21008 | C. | -21008 | D. | -22016 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [3,7] | B. | [4,6] | C. | [3,6] | D. | [4,7] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com