
分析 (Ⅰ)根据二倍角公式、两角差的正弦公式化简解析式,结合条件求出周期,由周期公式求出ω,将点$(\frac{π}{3},1)$代入解析式化简后,由内角的范围和特殊角的三角函数值求出φ,即可求出f(x);
(Ⅱ)由正弦定理和余弦定理化简已知的式子,利用两角和的正弦公式和内角的范围求出B,由解析式化简$f(A)=\frac{{1+\sqrt{3}}}{2}$,根据角A的范围和特殊角的三角函数值求出A,再由内角和定理求出C.
解答 解:(Ⅰ)由题意得,f(x)=$\frac{\sqrt{3}}{2}$sin(ωx+φ)+$\frac{1}{2}$[1-cos(ωx+φ)]
=$sin(ωx+φ-\frac{π}{6})+\frac{1}{2}$,
∵两个相邻对称中心的距离为$\frac{π}{2}$,则T=π,
∴$\frac{2π}{|ω|}=π$,且ω>0,解得ω=2,
又f(x)过点$(\frac{π}{3},1)$,∴$sin(2×\frac{π}{3}+φ-\frac{π}{6})+\frac{1}{2}=1$,
则$sin(\frac{π}{2}+φ)=\frac{1}{2}$,即cosφ=$\frac{1}{2}$,由0<φ<$\frac{π}{2}$得,φ=$\frac{π}{3}$,
∴f(x)=$sin(2x+\frac{π}{6})+\frac{1}{2}$;
(Ⅱ)在△ABC中,由余弦定理得b2=a2+c2-2accosB,
∴b2-a2-c2=-2accosB,
同理可得,c2-a2-b2=-2abcosC,
代入$\frac{sinC}{2sinA-sinC}=\frac{{b}^{2}-{a}^{2}-{c}^{2}}{{c}^{2}-{a}^{2}-{b}^{2}}$得,$\frac{sinC}{2sinA-sinC}=\frac{-2accosB}{-2abcosC}$=$\frac{ccosB}{bcosC}$,
由正弦定理得,$\frac{sinC}{2sinA-sinC}=\frac{sinCcosB}{sinBcosC}$,
由0<C<π得sinC≠0,∴sinBcosC=2sinAcosB-sinCcosB,
∴2sinAcosB=sinBcosC+sinCcosB=sin(B+C)=sinA,
由0<A<π得sinA≠0,化简得cosB=$\frac{1}{2}$,
∵0<B<π,∴B=$\frac{π}{3}$,
由$f(A)=\frac{{1+\sqrt{3}}}{2}$得$sin(2A+\frac{π}{6})+\frac{1}{2}=\frac{\sqrt{3}+1}{2}$,则$sin(2A+\frac{π}{6})=\frac{\sqrt{3}}{2}$,
∵$0<A<\frac{2π}{3}$,∴$\frac{π}{6}<2A+\frac{π}{6}<\frac{3π}{2}$,则$2A+\frac{π}{6}=\frac{π}{3}$或$2A+\frac{π}{6}=\frac{2π}{3}$,
解得$A=\frac{π}{12}$或$A=\frac{π}{4}$,
所以当$A=\frac{π}{12}$时,$C=\frac{7}{12}π$;当$A=\frac{π}{4}$时,$C=\frac{5}{12}π$.
点评 本题考查正弦定理、余弦定理的灵活应用,三角恒等变换的公式,考查化简、变形能力,注意内角的范围,属于中档题.


 应用题作业本系列答案
应用题作业本系列答案科目:高中数学 来源: 题型:填空题
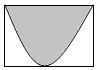 如图,长方形的面积为2,将100颗豆子随机地撒在长方形内,其中恰好有60 颗豆子落在阴影部分内,则用随机模拟的方法可以估计图中阴影部分的面积为$\frac{6}{5}$.
如图,长方形的面积为2,将100颗豆子随机地撒在长方形内,其中恰好有60 颗豆子落在阴影部分内,则用随机模拟的方法可以估计图中阴影部分的面积为$\frac{6}{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com