
设函数
(1)若 ,求函数
,求函数 在
在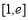 上的最小值;
上的最小值;
(2)若函数 在
在 存在单调递增区间,试求实数
存在单调递增区间,试求实数 的取值范围;
的取值范围;
(3)求函数 的极值点.
的极值点.
(1)最小值为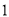 .(2)
.(2)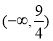 .
.
(3)当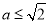 时,函数
时,函数 没有极值点;
没有极值点;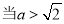 时,
时, 是函数
是函数 的极大值点;
的极大值点;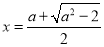 是函数
是函数 的极小值点.
的极小值点.
【解析】
试题分析:(1)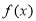 的定义域为
的定义域为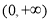 ,根据
,根据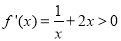 ,得
,得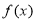 在
在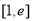 上增函数,当
上增函数,当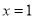 时,
时,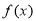 取得最小值
取得最小值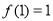 .
.
(2)由于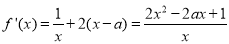 ,设
,设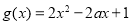 .
.
依题意,在区间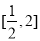 上存在子区间使得不等式
上存在子区间使得不等式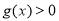 成立.
成立.
根据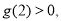 或
或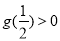 ,解得实数
,解得实数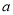 取值范围是
取值范围是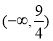 .
.
(3)由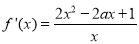 ,令
,令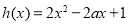 .分
.分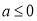 ,
,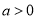 讨论
讨论 的符号及驻点情况.
的符号及驻点情况.
1)当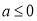 时,在
时,在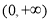 上
上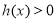 恒成立,
恒成立,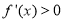 ,此时,函数
,此时,函数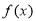 没有极值点.
没有极值点.
2)当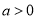 时,
时,
①当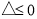 即
即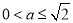 时,在
时,在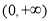 上
上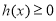 恒成立,这时
恒成立,这时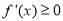 ,此时,函数
,此时,函数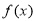 没有极值点.
没有极值点.
②当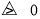 即
即 时,
时,
当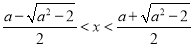 时,易知
时,易知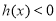 ,这时
,这时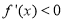 ;
;
当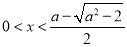 或
或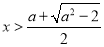 时,易知
时,易知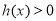 ,这时
,这时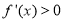 .
.
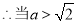 时,
时, 是函数
是函数 的极大值点;
的极大值点;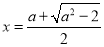 是函数
是函数 的极小值点.
的极小值点.
解答本题的主要难度在于转化思想与分类讨论思想的利用.
试题解析:(1)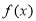 的定义域为
的定义域为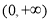 ,
,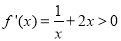 ,
,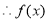 在
在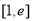 上增函数,当
上增函数,当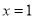 时,
时,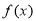 取得最小值
取得最小值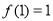 ,
,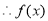 在
在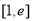 上的最小值为
上的最小值为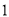 . 4分
. 4分
(2)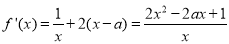 ,设
,设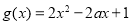 .
.
依题意,在区间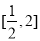 上存在子区间使得不等式
上存在子区间使得不等式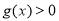 成立.
成立.
注意到抛物线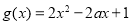 开口向上,所以只要
开口向上,所以只要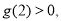 或
或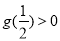 即可.
即可.
由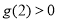 得
得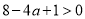 ,解得
,解得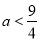 ,
,
由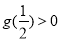 得
得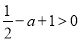 ,得
,得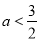 ,
,
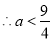 ,即实数
,即实数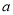 取值范围是
取值范围是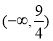 . 8分
. 8分
(3)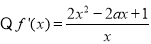 ,令
,令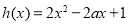 。
。
1)显然,当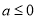 时,在
时,在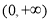 上
上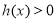 恒成立,这时
恒成立,这时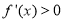 ,此时,函数
,此时,函数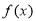 没有极值点.
没有极值点.
2)当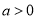 时,
时,
①当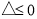 即
即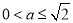 时,在
时,在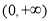 上
上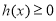 恒成立,这时
恒成立,这时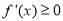 ,此时,函数
,此时,函数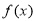 没有极值点.
没有极值点.
②当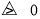 即
即 时,
时,
当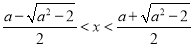 时,易知
时,易知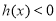 ,这时
,这时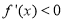 ;
;
当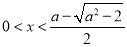 或
或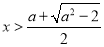 时,易知
时,易知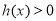 ,这时
,这时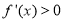 .
.
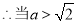 时,
时, 是函数
是函数 的极大值点;
的极大值点;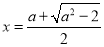 是函数
是函数 的极小值点.
的极小值点.
综上,当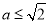 时,函数
时,函数 没有极值点;
没有极值点;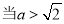 时,
时, 是函数
是函数 的极大值点;
的极大值点;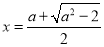 是函数
是函数 的极小值点. 13分
的极小值点. 13分
考点:应用导数研究函数的单调性、最(极)值,转化与化归思想,分类讨论思想.


科目:高中数学 来源:2013-2014学年湖南省长沙市高考二模文科数学试卷(解析版) 题型:选择题
 中,角
中,角 的对边分别为
的对边分别为 ,则“
,则“ ”是“
”是“ 是等腰三角形”的( )
是等腰三角形”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源:2013-2014学年湖南省益阳市高三模拟考试理科数学试卷(解析版) 题型:选择题
为了了解某校九年级1600名学生的体能情况,随机抽查了部分学生,测试1分钟仰卧起坐的成绩(次数),将数据整理后绘制成如图所示的频率分布直方图,根据统计图的数据,下列结论错误的是( )

A.该校九年级学生1分钟仰卧起坐的次数的中位数为26.25次
B.该校九年级学生1分钟仰卧起坐的次数的众数为27.5次
C.该校九年级学生1分钟仰卧起坐的次数超过30次的人数约有320人
D.该校九年级学生1分钟仰卧起坐的次数少于20次的人数约有32人
查看答案和解析>>
科目:高中数学 来源:2013-2014学年湖南省益阳市高三模拟考试文科数学试卷(解析版) 题型:解答题
在 中,角A,B,C的对边分别为a,b,c,已知
中,角A,B,C的对边分别为a,b,c,已知 ,
, .
.
(1)求 的值;
的值;
(2)若 为
为 的中点,求
的中点,求 、
、 的长.
的长.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年湖南省益阳市高三模拟考试文科数学试卷(解析版) 题型:选择题
已知函数 ,若存在正实数k,使得方程
,若存在正实数k,使得方程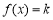 在区间
在区间 上有三个互不相等的实数根
上有三个互不相等的实数根 ,则x1+x2+x3的取值范围是 ( )
,则x1+x2+x3的取值范围是 ( )
A. B.
B. C.
C. D.
D. 
查看答案和解析>>
科目:高中数学 来源:2013-2014学年湖南省怀化市高三第二次模拟考试理科数学试卷(解析版) 题型:填空题
有 名同学站成一排,要求甲、乙两名同学必须相邻,有____种不同的站法(用数字作答).
名同学站成一排,要求甲、乙两名同学必须相邻,有____种不同的站法(用数字作答).
查看答案和解析>>
科目:高中数学 来源:2013-2014学年湖北省黄冈市高三5月适应性考试理科数学试卷(解析版) 题型:填空题
(坐标系与参数方程选做题)已知直线的极坐标方程为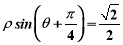 ,则点A(2,
,则点A(2,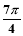 )到这条直线的距离为 .
)到这条直线的距离为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com