
| 男性 | 女性 | 合计 | |
| 做不到“光盘” | 18 | ||
| 能做到“光盘” | 14 | ||
| 合 计 | 50 |
分析 (Ⅰ)根据题意,补全相应的2×2列联表即可;
(Ⅱ)计算k2的观测值,对照数表即可得出正确的概率结论.
解答 解:(Ⅰ)补全相应的2×2列联表,如下;
| 男性 | 女性 | 合计 | |
| 做不到“光盘” | 18 | 11 | 29 |
| 能做到“光盘” | 7 | 14 | 21 |
| 合 计 | 25 | 25 | 50 |
点评 本题考查了2×2列联表与独立性检验的意义问题,是基础题目.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
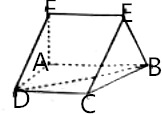 如图,在直角梯形ABCD中,AB∥CD,∠DAB=90°,AD=CD=$\frac{1}{2}$AB=1,直角梯形ABEF可以通过直角梯形ABCD以直线AB为轴旋转得到,且平面ABEF⊥平面ABCD
如图,在直角梯形ABCD中,AB∥CD,∠DAB=90°,AD=CD=$\frac{1}{2}$AB=1,直角梯形ABEF可以通过直角梯形ABCD以直线AB为轴旋转得到,且平面ABEF⊥平面ABCD查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,+∞) | B. | (-∞,1] | C. | [-1,+∞) | D. | (-∞,-1] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,4] | B. | (-∞,2] | C. | [4,+∞) | D. | [2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com