
分析 (1)求出f(x)定义域为(0,+∞),f′(x)=$\frac{1-lnx}{x2}$.令f'(x)=$\frac{1-lnx}{x2}$=0,得x=e.由此列表讨论经,能求出函数f(x)的最小值.
(2)f(x) g(x)≤0恒成立,即2ln x-ax+a≤0在x>0时恒成立.令h(x)=f(x) g(x),则h′(x)=$\frac{2-ax}{x}$,x>0.由此利用导数性质及分类讨论思想能求出a.
(3)研究函数图象,f(x)在(0,e)上单调递增,在(e,+∞)上单调递减.由此得到总存在正实数m,n,且1<m<e<n,使得mn=nm.
解答 解:(1)∵函数f(x)=$\frac{lnx}{x}$,
∴f(x)定义域为(0,+∞),f′(x)=$\frac{1-lnx}{x2}$.
令f'(x)=$\frac{1-lnx}{x2}$=0,则x=e.
列表如下:
| x | (0,e) | e | (e,+∞) |
| f'(x) | + | 0 | - |
| f(x) | ↗ | $\frac{1}{e}$ | ↘ |
点评 本题考查函数的最小值的求法,考查实数的取值范围的求法,考查满足条件的正实数是否存在的判断,是中档题,解题时要认真审题,注意导数性质的、分类讨论思想的合理运用.


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 男性 | 女性 | 合计 | |
| 做不到“光盘” | 18 | ||
| 能做到“光盘” | 14 | ||
| 合 计 | 50 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图所示是y=f(x)的导数图象,则正确的判断是( )
如图所示是y=f(x)的导数图象,则正确的判断是( )| A. | ①②④ | B. | ②④ | C. | ③④ | D. | ①③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,在平行四边形ABCD中,点E在AB上且EB=2AE,AC与DE交于点F,则△CDF的周长与△AEF的周长之比为( )
如图,在平行四边形ABCD中,点E在AB上且EB=2AE,AC与DE交于点F,则△CDF的周长与△AEF的周长之比为( )| A. | 1:3 | B. | 3:1 | C. | 1:2 | D. | 2:1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
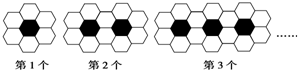
| A. | 8064块 | B. | 8066块 | C. | 8068块 | D. | 8070块 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
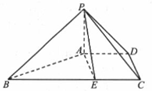 如图,四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为梯形,AD∥BC,BC=6,PA=AD=CD=2,E为BC上一点且BE=$\frac{2}{3}$BC,PB⊥AE.
如图,四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为梯形,AD∥BC,BC=6,PA=AD=CD=2,E为BC上一点且BE=$\frac{2}{3}$BC,PB⊥AE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com