
���� ��1������ҽ���Ͷ�������꣬�������ʹ�ʽ��ƽ�����������������ʾ���ⷽ�̿ɵ�a��b��c�������õ���Բ���̣�
��2����A��x1��y1����B��x2��y2����N��x0��0���������������������ʾ����ֱ��l�ķ���Ϊy=kx-1��k��0������������x2+4y2=8������Τ�ﶨ���ͽⷽ�̣��õ�k�ķ��̣����ɵõ�����ֱ�߷��̣�ע������б�ʽ����0��
��� �⣺��1������Բ���ҽ���F ��c��0����c��0����B1��0��b����B2��0��-b����
��$\overrightarrow{F{B}_{1}}$•$\overrightarrow{F{B}_{2}}$=4������-c��b��•��-c��-b��=c2-b2=4������3�֣�
��������$\frac{c}{a}$=$\frac{\sqrt{3}}{2}$��a2-b2=c2��
���a=2$\sqrt{2}$��b=$\sqrt{2}$������5�֣�
����Բ�ķ���Ϊ$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{2}$=1������6�֣�
��2����A��x1��y1����B��x2��y2����N��x0��0����
��Ϊ$\overrightarrow{NA}$=-$\frac{7}{5}$$\overrightarrow{NB}$�����ԣ�x1-x0��y1��=-$\frac{7}{5}$��x2-x0��y2����y1=-$\frac{7}{5}$y2����
��֪��ֱ��l��б�ʲ����ڻ�б��Ϊ0ʱ���ٲ�����������8�֣�
������ֱ��l�ķ���Ϊy=kx-1��k��0������������x2+4y2=8��
��ȥx�ã�4k2+1��y2+2y+1-8k2=0���ڡ���10�֣�
��Ϊ����0������ֱ������Բ�ཻ������y1+y2=-$\frac{2}{1+4{k}^{2}}$����
y1y2=$\frac{1-8{k}^{2}}{1+4{k}^{2}}$����
�ɢ٢۵ã�y2=$\frac{5}{1+4{k}^{2}}$��y1=-$\frac{7}{1+4{k}^{2}}$��
�����������8k4+k2-9=0��k2=1��k=��1��
����ֱ��l�ķ�����y=x-1��y=-x-1������12�֣�
���� ���⿼����Բ���̺�ֱ�߷��̵���ע�����������ʹ�ʽ��ֱ������Բ��������������Τ�ﶨ�������黯���������������������е��⣮


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ƽ��ABCD��ƽ��ABE������ABCDΪ���Σ���ABEΪֱ�������Σ���AEB=90�㣬AB=2AD=2AE=2��
��ͼ��ƽ��ABCD��ƽ��ABE������ABCDΪ���Σ���ABEΪֱ�������Σ���AEB=90�㣬AB=2AD=2AE=2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
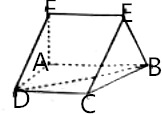 ��ͼ����ֱ������ABCD�У�AB��CD����DAB=90�㣬AD=CD=$\frac{1}{2}$AB=1��ֱ������ABEF����ͨ��ֱ������ABCD��ֱ��ABΪ����ת�õ�����ƽ��ABEF��ƽ��ABCD
��ͼ����ֱ������ABCD�У�AB��CD����DAB=90�㣬AD=CD=$\frac{1}{2}$AB=1��ֱ������ABEF����ͨ��ֱ������ABCD��ֱ��ABΪ����ת�õ�����ƽ��ABEF��ƽ��ABCD�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | e3f��-14����f��-5����e3f��-10����f��-19�� | B�� | e3f��-14����f��-5����e3f��-10����f��-19�� | ||
| C�� | e3f��-14����f��-5����e3f��-10����f��-19�� | D�� | e3f��-14����f��-4����e3f��-10����f��-19�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -1 | B�� | 0 | C�� | -$\frac{4}{3}$ | D�� | -$\frac{13}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | [1��+�ޣ� | B�� | ��-�ޣ�1] | C�� | [-1��+�ޣ� | D�� | ��-�ޣ�-1] |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com