
| A. | -1 | B. | 0 | C. | -$\frac{4}{3}$ | D. | -$\frac{13}{3}$ |
分析 求出函数的导数,利用函数的极值求出a,b,然后判断函数的单调性,求解函数在闭区间上的最值即可.
解答 解:f'(x)=-x2+2x+a,由题意知$\left\{\begin{array}{l}f'(3)=0\\ f(3)=4\end{array}\right.$,
即$\left\{\begin{array}{l}-9+6+a=0\\-\frac{1}{3}×27+{3^2}+3a+b=4\end{array}\right.$,解答$\left\{\begin{array}{l}a=3\\ b=-5\end{array}\right.$.
∴$f(x)=-\frac{1}{3}{x^3}+{x^2}+3x-5$,f'(x)=-x2+2x+3,
由f'(x)=-x2+2x+3=0得x=-1,x=3,
∴函数f(x)在区间[-2,-1]递减,在区间[-1,1]递增.
又$f(1)=-\frac{4}{3}$,$f(-1)=-\frac{13}{3}$,
所以 f(x)在区间[-2,1]上的最大值为$-\frac{4}{3}$.
故选:C.
点评 本题考查函数的导数的应用,函数的单调性以及函数的极值的应用,考查转化思想以及计算能力.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源: 题型:选择题
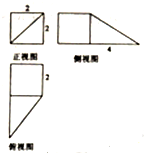
| A. | $\frac{40}{3}$ | B. | 40 | C. | $\frac{20}{3}$ | D. | 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{8π}{3}$ | B. | $\frac{32π}{3}$ | C. | 8π | D. | $\frac{8\sqrt{2}π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a=b=1 | B. | a=1,b=2 | C. | a=2,b=1 | D. | 不存在这样的a,b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com