
下列四个命题:
①若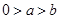 ,则
,则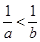 ;
;
②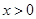 ,
,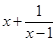 的最小值为
的最小值为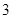 ;
;
③椭圆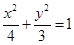 比椭圆
比椭圆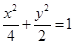 更接近于圆;
更接近于圆;
④设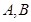 为平面内两个定点,若有
为平面内两个定点,若有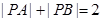 ,则动点
,则动点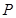 的轨迹是椭圆;
的轨迹是椭圆;
其中真命题的序号为________________.(写出所有真命题的序号)
 名题金卷系列答案
名题金卷系列答案科目:高中数学 来源: 题型:填空题
下列说法中正确的是 .
①“若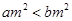 ,则
,则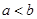 ”的逆命题为真;
”的逆命题为真;
②线性回归方程对应的直线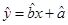 一定经过其样本数据点
一定经过其样本数据点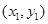 ,
, ,
,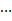 ,
, 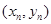 中的一个点;
中的一个点;
③命题“存在实数 ,使得
,使得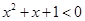 ”的否定是“对任意实数
”的否定是“对任意实数 ,均有
,均有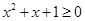 ”
”
④用数学归纳法证明(n+1)(n+2)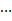 (n+n)=
(n+n)= 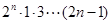 (
(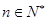 )时,从“k”到“k+1”的证明,左边需增添的一个因式是2(2k+1).
)时,从“k”到“k+1”的证明,左边需增添的一个因式是2(2k+1).
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
①由“若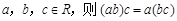 ”类比“若
”类比“若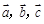 为三个向量,则
为三个向量,则 ”;②设圆
”;②设圆 与坐标轴的4个交点分别为A (x1,0)、B (x2,0)、C (0,y1)、D (0,y2),则
与坐标轴的4个交点分别为A (x1,0)、B (x2,0)、C (0,y1)、D (0,y2),则 ;③在平面内“三角形的两边之和大于第三边”类比在空间中“四面体的任意三个面的面积之和大于第四个面的面积”;④在实数列
;③在平面内“三角形的两边之和大于第三边”类比在空间中“四面体的任意三个面的面积之和大于第四个面的面积”;④在实数列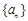 中,已知a1 = 0,
中,已知a1 = 0,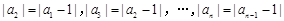 ,则
,则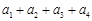 的最大值为2.上述四个推理中,得出的结论正确的是_____________(写出所有正确结论的序号).
的最大值为2.上述四个推理中,得出的结论正确的是_____________(写出所有正确结论的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
下列叙述正确的序号是 。
(1)对于定义在R上的函数 ,若
,若 ,则函数
,则函数 不是奇函数;
不是奇函数;
(2) 定义在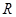 上的函数
上的函数 ,在区间
,在区间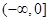 上是单调增函数,在区间
上是单调增函数,在区间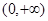 上也是单调增函数,则函数
上也是单调增函数,则函数 在
在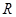 上是单调增函数;
上是单调增函数;
(3) 已知函数的解析式为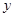 =
=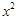 ,它的值域为
,它的值域为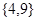 ,那么这样的函数有9个;
,那么这样的函数有9个;
(4)对于任意的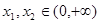 ,若函数
,若函数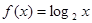 ,则
,则
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
已知定义域为 的函数
的函数 满足:①对任意
满足:①对任意 ,恒有
,恒有 成立;当
成立;当 时,
时,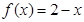 。给出如下结论:
。给出如下结论:
①对任意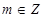 ,有
,有 ;②函数
;②函数 的值域为
的值域为 ;③存在
;③存在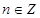 ,使得
,使得 ;④“函数
;④“函数 在区间
在区间 上单调递减”的充要条件是 “存在
上单调递减”的充要条件是 “存在 ,使得
,使得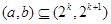 ”。其中所有正确结论的序号是 。
”。其中所有正确结论的序号是 。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com