
分析 直接利用数学归纳法的证明步骤,n=1时验证不等式成立,假设n=k时不等式成立,然后证明n=k+1时,不等式也成立.
解答 证明:利用数学归纳法证明.
①当n=1时,左边=1,右边=2,左边<右边,不等式成立;
②假设n=k时,不等式成立,即1+22+33+…+kk<(k+1)k.
那么当n=k+1时,1+22+33+…+kk+(k+1)k+1<(k+1)k+(k+1)k+1=(k+1)k(1+k+1)=(k+1)k(k+2)<(k+2)k(k+2)<(k+2)k+1,
这就是说,n=k+1时,不等式也成立.
由①②可知,当n∈N+时,1+22+33+…+nn<(n+1)n.
点评 本题考查数列在不等式证明中的应用,考查数学归纳法的证明步骤,注意用上假设是证明问题的关键,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
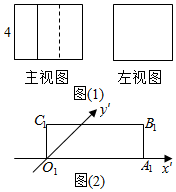 某几何体的主视图和左视图如图(1),它的俯视图的直观图是矩形O1A1B1C1如图(2),其中O1A1=6,O1C1=2,则该几何体的侧面积为( )
某几何体的主视图和左视图如图(1),它的俯视图的直观图是矩形O1A1B1C1如图(2),其中O1A1=6,O1C1=2,则该几何体的侧面积为( )| A. | 48 | B. | 64 | C. | 96 | D. | 128 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3个 | B. | 2个 | C. | 1个 | D. | 0个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | 11 | C. | 15 | D. | 不存在 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com