
| A. | $10\sqrt{2}a$ | B. | 10a | C. | $(5+\sqrt{5})a$ | D. | $12\sqrt{2}a$ |
分析 求出E,P,Q的坐标,利用距离公式,即可得出结论.
解答 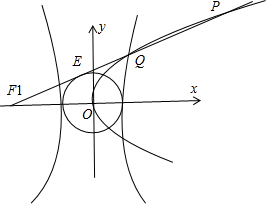 解:设直线的倾斜角为α,则由题意$\frac{c}{a}$=$\sqrt{3}$,∴sinα=$\frac{\sqrt{3}}{3}$,
解:设直线的倾斜角为α,则由题意$\frac{c}{a}$=$\sqrt{3}$,∴sinα=$\frac{\sqrt{3}}{3}$,
∴tanα=$\frac{\sqrt{2}}{2}$,
切线方程为y=$\frac{\sqrt{2}}{2}$(x+c),代入y2=4cx,
可得x2-6cx+c2=0,∴x=(3±2$\sqrt{2}$)c,
∴P((3+2$\sqrt{2}$)c,(2$\sqrt{2}$+2)c),
Q((3-2$\sqrt{2}$)c,(2$\sqrt{2}$-2)c),
直线OE与PE的方程分别为y=-$\sqrt{2}$x与y=$\frac{\sqrt{2}}{2}$(x+c),
联立可得E(-$\frac{1}{3}$c,$\frac{\sqrt{2}}{3}$c),
∴|PE|+|QE|=$\sqrt{(\frac{10}{3}+2\sqrt{2})^{2}+(\frac{5\sqrt{2}}{3}+2)^{2}}$c+$\sqrt{(\frac{10}{3}-2\sqrt{2})^{2}+(\frac{5\sqrt{2}}{3}-2)^{2}}$c=($\frac{5\sqrt{2}}{3}$+2)c+($\frac{5\sqrt{2}}{3}$-2)c=$\frac{10\sqrt{2}}{3}$c=10$\sqrt{2}$a,
故选A.
点评 本题考查直线与圆、抛物线的位置关系,考查学生的计算能力,属于中档题.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:选择题
| A. | (-∞,4) | B. | [1,2] | C. | [2,4] | D. | (2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | $(-\sqrt{2},\sqrt{2})$ | C. | (-1,1) | D. | [-1,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com